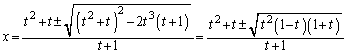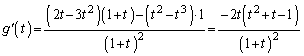���l����H���w'09�N���[3]
xy���ʏ�̗̈� �C
�C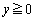 �ŁA������
�ŁA������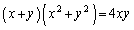 ���\���Ȑ���C�Ƃ���B���̐�t�ɑ��āA����
���\���Ȑ���C�Ƃ���B���̐�t�ɑ��āA����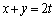 ��C�ƈقȂ�2�_Q�CR�Ō����Ƃ��A���̖₢�ɓ�����B
��C�ƈقȂ�2�_Q�CR�Ō����Ƃ��A���̖₢�ɓ�����B
(1) C���ɍ��W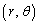 �Ɋւ���������ŕ\���Ar�̂Ƃ蓾��l�̍ő�l�����߂�B
�Ɋւ���������ŕ\���Ar�̂Ƃ蓾��l�̍ő�l�����߂�B (2) Q�CR�̍��W��t��p���ĕ\���B
(3) ����QR�̒������ő�ƂȂ�t�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ȃ��Ȃ��f���ɍs���Ȃ������̌v�Z���ł��B
(1) C�F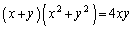 �@����@
�@����@ �ɁA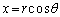 �C
�C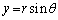 (
(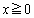 �C
�C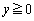 ���A
���A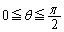 )��������(�ɍ��W���Q��)�ƁA
)��������(�ɍ��W���Q��)�ƁA �� 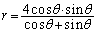 �@����A
�@����A
�����ŁA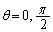 �Ƃ����
�Ƃ����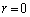 (��)�ƂȂ�̂ŁA�A��
(��)�ƂȂ�̂ŁA�A�� �̏ꍇ���܂�ł��܂��B
�̏ꍇ���܂�ł��܂��B
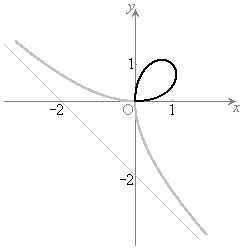 ���D���s�̍��Z�̋��ȏ��ł�
���D���s�̍��Z�̋��ȏ��ł�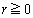 �ł��邱�Ƃ��z�肳��Ă��āA
�ł��邱�Ƃ��z�肳��Ă��āA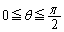 �͈̔͂ɂ����ẮA�A��
�͈̔͂ɂ����ẮA�A��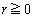 �ƂȂ�܂��B�ł����A
�ƂȂ�܂��B�ł����A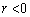 ���������Ƃɂ���(��2�ی��A��3�ی��̕����ɂ��O���t���ł��܂�)�ƁA�ɕ������A�̕\���Ȑ��͉E�}�̂悤�ɂȂ�܂��B�Ȑ�C�ɓ����镔���������A����ȊO�̕������D�F�̐��ŕ`���܂����B
���������Ƃɂ���(��2�ی��A��3�ی��̕����ɂ��O���t���ł��܂�)�ƁA�ɕ������A�̕\���Ȑ��͉E�}�̂悤�ɂȂ�܂��B�Ȑ�C�ɓ����镔���������A����ȊO�̕������D�F�̐��ŕ`���܂����B
�A�̉E�ӂ�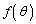 �Ƃ����ƁA
�Ƃ����ƁA ���̕��q�́A
�� 
 ���A
���A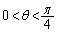 �ɂ�����
�ɂ����� ��
��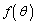 �͑����A
�͑����A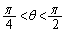 �ɂ�����
�ɂ����� ��
��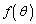 �͌���(���̑������Q��)�B����āA
�͌���(���̑������Q��)�B����āA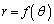 (
(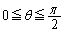 )�̍ő�l�́A
)�̍ő�l�́A 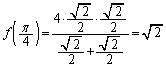 ......[��]
......[��]
(2) �@��ό`���āA
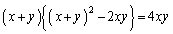
 �@����B
�@����B�������āA
�B���A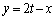
�������āA
�� 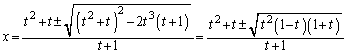 ���قȂ�2�����������̂́A������(���ʎ�)�����̂Ƃ�(2�����������Q��)�A�܂�A
���قȂ�2�����������̂́A������(���ʎ�)�����̂Ƃ�(2�����������Q��)�A�܂�A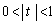 �̂Ƃ��ŁA��蕶��
�̂Ƃ��ŁA��蕶�� �Ƃ����w��ɂ��A
�Ƃ����w��ɂ��A
���̂Ƃ��A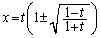 �C
�C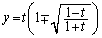 (��������)����āA��_Q�CR�̍��W�́A
(��������)����āA��_Q�CR�̍��W�́A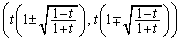 (��������) ......[��]
(��������) ......[��]
(3) �����B�̌X����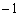 �Ȃ̂ŁA����QR�̒����́AQ�CR��x���W�̍��̐�Βl��
�Ȃ̂ŁA����QR�̒����́AQ�CR��x���W�̍��̐�Βl��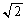 �{(�����̕��������Q��)�ŁA
�{(�����̕��������Q��)�ŁA �Ƃ����ƁA
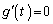 �Ƃ���ƁA
�Ƃ���ƁA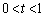 �ɂ����ẮA
�ɂ����ẮA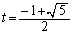
 �ɂ�����
�ɂ�����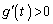 ��
��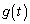 �͑����A
�͑����A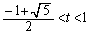 �ɂ�����
�ɂ�����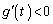 ��
��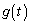 �͌����B����āA����QR�̒����A�����A
�͌����B����āA����QR�̒����A�����A ���ő�Ƃ���t�̒l�́A
���ő�Ƃ���t�̒l�́A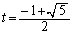 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 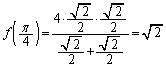 ......[��]
......[��]