���l����o�ϐ��w'09�N[2]
����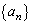 �C
�C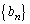 �C
�C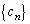 ��
��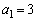 �C
�C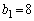 �C
�C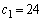 �ƊW��
�ƊW��
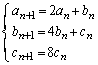 �@
�@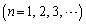
(1) 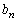 ��n�̎��ŕ\���B
��n�̎��ŕ\���B (2) 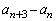 ��7�Ŋ����邱�Ƃ������A
��7�Ŋ����邱�Ƃ������A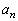 ��7�Ŋ����邽�߂�n�̏��������߂�B
��7�Ŋ����邽�߂�n�̏��������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)������̂ŁA(2)�ł�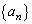 �̈�ʍ������߂����Ȃ�܂����A(1)�������Ƃ�(2)�����ŒP�Ƃʼn��邱�Ƃ��\�ł��B
�̈�ʍ������߂����Ȃ�܂����A(1)�������Ƃ�(2)�����ŒP�Ƃʼn��邱�Ƃ��\�ł��B
�Ȃ��A(1)�ɂ��ẮA�Q�����̋Z�I���Q�Ƃ��Ă��������B
(1) 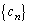 �́A�����F24�C����F8�����䐔���Ȃ̂ŁA
�́A�����F24�C����F8�����䐔���Ȃ̂ŁA ���ӂ�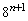 �Ŋ���A
�Ŋ���A 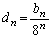 �@����@ �Ƃ����ƁA
�@����@ �Ƃ����ƁA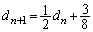 �@����A
�@����A
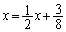 �@����B
�@����B�B�������āA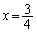
�A�|�B���A ������A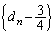 �́A�����F
�́A�����F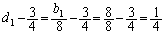 �C����F
�C����F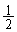 �̓��䐔��Ȃ̂ŁA
�̓��䐔��Ȃ̂ŁA �@���A
��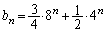 ......[��]
......[��]
(2) �^����ꂽ�Q�����̑�1���ō��ԍ���1���炷���Ƃɂ��A
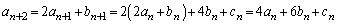 �@����C
�@����C����ɍ��ԍ���1���点�āA
�� 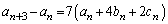 �@����D
�@����D
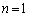 �̂Ƃ��A
�̂Ƃ��A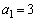 �C
�C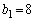 �C
�C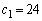 �͐����ł����āA
�͐����ł����āA
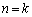 �̂Ƃ��A
�̂Ƃ��A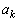 �C
�C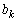 �C
�C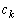 �������ł���A�^����ꂽ�Q�������A
�������ł���A�^����ꂽ�Q�������A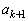 �C
�C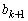 �C
�C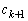 �������ŁA���w�I�A�[�@�ɂ��A���ׂĂ̎��R��n�ɂ��āA
�������ŁA���w�I�A�[�@�ɂ��A���ׂĂ̎��R��n�ɂ��āA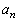 �C
�C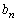 �C
�C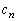 �͐����ł��B
�͐����ł��B
����āA�D����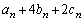 �������ł���A
�������ł���A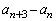 ��7�̔{���ł��B�@���(��)�^����ꂽ�Q�����̑�1����
��7�̔{���ł��B�@���(��)�^����ꂽ�Q�����̑�1����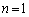 �Ƃ��āA
�Ƃ��āA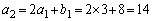
�C��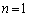 �Ƃ��āA
�Ƃ��āA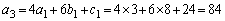
�����̂��Ƃ���Am��1�ȏ�̐����Ƃ��āA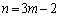 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�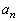 ��7�Ŋ���ꂸ�A
��7�Ŋ���ꂸ�A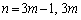 �̂Ƃ���7�Ŋ�����Ɨ\���ł��܂��B�ȉ��A���̗\����m�Ɋւ��鐔�w�I�A�[�@�Ŏ����܂��B
�̂Ƃ���7�Ŋ�����Ɨ\���ł��܂��B�ȉ��A���̗\����m�Ɋւ��鐔�w�I�A�[�@�Ŏ����܂��B
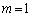 �̂Ƃ��A
�̂Ƃ��A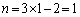 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�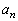 (
(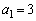 )��7�Ŋ���ꂸ�A
)��7�Ŋ���ꂸ�A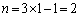 �C
�C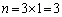 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�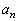 ��(
��(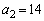 �C
�C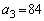 )7�Ŋ�����̂ŁA�\���͐������܂��B
)7�Ŋ�����̂ŁA�\���͐������܂��B
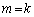 �̂Ƃ��A�\������������Ɖ��肷��ƁA
�̂Ƃ��A�\������������Ɖ��肷��ƁA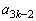 ��7�Ŋ���ꂸ�A
��7�Ŋ���ꂸ�A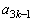 �C
�C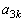 ��7�Ŋ����܂��B���̂Ƃ��A(��)���A
��7�Ŋ����܂��B���̂Ƃ��A(��)���A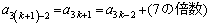 ��7�Ŋ���ꂸ�A
��7�Ŋ���ꂸ�A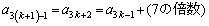 �C
�C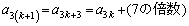 ��7�Ŋ�����̂ŁA�\����
��7�Ŋ�����̂ŁA�\����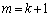 �̂Ƃ��ɂ��������܂��B
�̂Ƃ��ɂ��������܂��B
�ȏ���A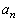 ��7�Ŋ����邽�߂�n�̏����́A
��7�Ŋ����邽�߂�n�̏����́A
�gn��3�Ŋ������Ƃ��̗]�肪1�łȂ����R���ł��邱�Ɓh ......[��]�ʉ��D��L��(2)�ł́A(1)���g�킸�A�^����ꂽ�Q����������p���ĉ��܂������A�������A(1)�̌��ʂ𗘗p���Ă��A�܂��A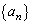 �̈�ʍ������߂Ă��A�ł��܂��B(1)�̌��ʂ𗘗p����̂ł���A
�̈�ʍ������߂Ă��A�ł��܂��B(1)�̌��ʂ𗘗p����̂ł���A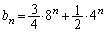 ��^����ꂽ�Q�����̑�1���ɑ�����āA
��^����ꂽ�Q�����̑�1���ɑ�����āA 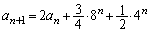 �@����E
�@����E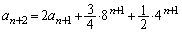
����ŁA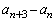 ��7�Ŋ����邱�Ƃ������܂��B
��7�Ŋ����邱�Ƃ������܂��B
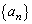 �̈�ʍ������߂�̂ł���A�E��
�̈�ʍ������߂�̂ł���A�E��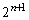 �Ŋ���A
�Ŋ���A ����́A����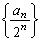 ���K��������
���K��������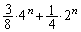 �ł��邱�Ƃ��Ӗ����܂��B����āA
�ł��邱�Ƃ��Ӗ����܂��B����āA 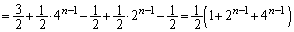 �@(
�@(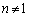 )
)�� 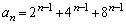 �@(
�@(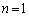 �̂Ƃ������藧���܂�)
�̂Ƃ������藧���܂�) ����ŁA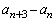 ��7�Ŋ����邱�Ƃ������܂��B
��7�Ŋ����邱�Ƃ������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@
�@