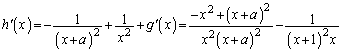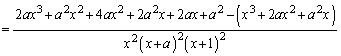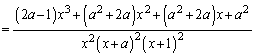������H���w'09�N���[5]
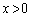 �Œ�`���ꂽ��
�Œ�`���ꂽ��
���l����B�������Aa�͒萔�ł���B���̖₢�ɓ�����B
(1)  �̂Ƃ��A
�̂Ƃ��A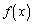 �͑������ł��邱�Ƃ������B
�͑������ł��邱�Ƃ������B (2)  �̂Ƃ��A
�̂Ƃ��A �͌������ł��邱�Ƃ������B
�͌������ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̕ϓN���Ȃ����ς̌v�Z���Ɍ�����̂ł����A(2)���ӊO�ɖ��ł��B
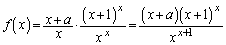 �@(
�@(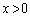 )
)

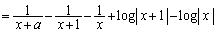 �@����@
�@����@�ǂ��ł������悤�Ɍ����܂����A(2)���ɂ��ŁA�������₷���悤�ɁA���q���ł��邾���ȒP�Ȍ`�ɂ��Ă����̂��A���̖��̃|�C���g�ł��B
(1) 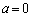 �̂Ƃ��A
�̂Ƃ��A  (
(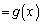 �Ƃ����܂�)
�Ƃ����܂�)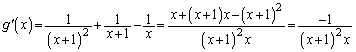 �@����A
�@����A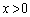 �ɂ����āA
�ɂ����āA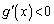 �Ȃ̂�
�Ȃ̂�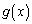 ���P�������ł��B�܂��A
���P�������ł��B�܂��A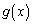 �͘A���Ȋ��ł��B
�͘A���Ȋ��ł��B
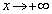 �̂Ƃ��A
�̂Ƃ��A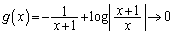 �@(���̋Ɍ����Q��)����āA
�@(���̋Ɍ����Q��)����āA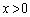 �ɂ�����
�ɂ�����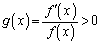 �ł��B
�ł��B
 �C
�C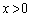 �̂Ƃ��A
�̂Ƃ��A �@����B
�@����B
����āA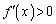 �C�]���āA
�C�]���āA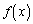 �͑������ł��B
�͑������ł��B
(2) �@���A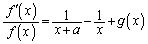 (
( �Ƃ����܂�)
�Ƃ����܂�) �A��p���āA
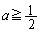 ���A���q�e���̌W���͐��܂���0�Ȃ̂ŁA
���A���q�e���̌W���͐��܂���0�Ȃ̂ŁA �ɂ����ĕ��q�͐��ł��B����āA
�ɂ����ĕ��q�͐��ł��B����āA �Ȃ̂ŁA
�Ȃ̂ŁA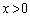 �ɂ����āA
�ɂ����āA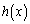 �͒P�������ł��B�܂��A
�͒P�������ł��B�܂��A �͘A���Ȋ��ł��B
�͘A���Ȋ��ł��B
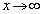 �̂Ƃ��A
�̂Ƃ��A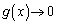 ���
���
����āA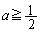 �̂Ƃ��A
�̂Ƃ��A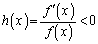 �ł��B
�ł��B
�B���A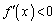 �C�]���āA
�C�]���āA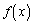 �͌������ł��B
�͌������ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 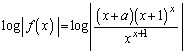
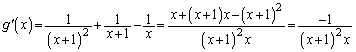 �@����A
�@����A