������H���w'09�N[4]
������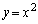 ���2�_P
���2�_P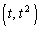 �CQ
�CQ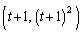 ���Ƃ�B���̖₢�ɓ�����B
���Ƃ�B���̖₢�ɓ�����B
(1) t�����ׂĂ̎������Ƃ��A����PQ���ʉ߂���̈�����߂�B
(2) t�� �͈̔͂��Ƃ��A����PQ���ʉ߂���̈�����߁A�}������B
�͈̔͂��Ƃ��A����PQ���ʉ߂���̈�����߁A�}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@xy���ʏ�ɂ����钼���̕������A���邢�́A�Ȑ��̕�������x�Cy�ȊO�̏��ϐ����܂�ł��āA���̏��ϐ������낢��Ȓl���Ƃ�A�Ƃ����ݒ�̖�肪����܂��B���̂Ƃ��A���ϐ��̒l���ω�����ƁA������Ȑ���xy���ʏ�����̂ł����A�������͈͂����߂����A�Ƃ����ꍇ�̑Ώ��@���A���̖��ōl���Ă݂܂��B
(2)�́A�u����PQ�v�̒ʉߔ͈͂ł͂Ȃ��A�u����PQ�v�̒ʉߔ͈͂Ȃ̂ŁAx�͈̔́At�͈̔͂����G�ɂ����ŁA���낢��ƌ������邱�Ƃ�����A������Ƃ�낤�Ƃ���Ɠ��ł��B
�������āA
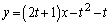 �@����@
�@����@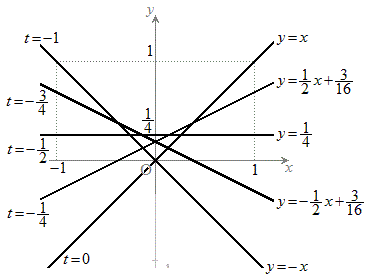
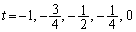 �̊e�l�ɑ��钼��PQ���E�}�Ɏ����܂��B����Ŗ��̊T���͂��߂܂��B
�̊e�l�ɑ��钼��PQ���E�}�Ɏ����܂��B����Ŗ��̊T���͂��߂܂��B
(1) t�����ׂĂ̎������Ƃ��ĕω�����Ƃ��ɒ����@���ʉ߂���̈�����߂�A�Ƃ������Ȃ̂ł����A�et�̒l�ɑ��Ē������ǂ������������悤�Ƃ���ƁA�T���͂��߂܂����A���m�ȋc�_�͂ł��܂���B
�@��x�̊��ƌ���̂ł͂Ȃ��Ax���W���Œ肵��t��2�����ƌ��邱�Ƃɂ��A����x���W�̂Ƃ����y���W���ǂ������͈͂̒l���Ƃ�̂��A�Ƃ�������������悤�ɂ��܂��B
�@�̉E�ӂ�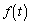 �Ƃ����ƁA
�Ƃ����ƁA 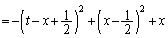
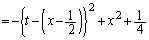 �@����A
�@����At�����ׂĂ̎������Ƃ��A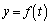 ��
��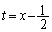 �ɂ����čő�l
�ɂ����čő�l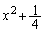 ���Ƃ�A�ő�l�ȉ��̂��ׂĂ̒l���Ƃ�܂��B
���Ƃ�A�ő�l�ȉ��̂��ׂĂ̒l���Ƃ�܂��B
�� 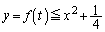
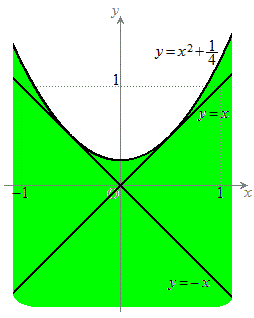 �ex���W�ɂ�����y���W��
�ex���W�ɂ�����y���W��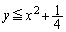 �Ƃ����͈͂̒l���Ƃ肤��A�Ƃ������Ƃ́Ax���W�����ƁA�����@�͗̈�F
�Ƃ����͈͂̒l���Ƃ肤��A�Ƃ������Ƃ́Ax���W�����ƁA�����@�͗̈�F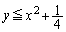 ���Ƃ������Ƃł��B����PQ���ʉ߂���̈�́A
���Ƃ������Ƃł��B����PQ���ʉ߂���̈�́A 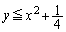 ......[��]�@(�}������ƉE�}���ΐF���F��(���E�����܂�))
......[��]�@(�}������ƉE�}���ΐF���F��(���E�����܂�))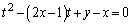 �@����B
�@����B�ƌ��āAt�������ł��邱�Ƃ���A���ꂪ�A���������������A
���ʎ��F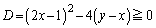
�� 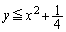 �Ƃ��ė̈�����߂邱�Ƃ��ł��܂��B
�Ƃ��ė̈�����߂邱�Ƃ��ł��܂��B
(2) t�� �͈̔͂��Ƃ��ɂ́A����PQ�̒ʉߔ͈͂��l���邽�߂ɂ́A�A�ŗ^�������
�͈̔͂��Ƃ��ɂ́A����PQ�̒ʉߔ͈͂��l���邽�߂ɂ́A�A�ŗ^�������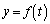 ��
�� �͈̔͂ɂ����ĂƂ肤��l���l���邱�ƂɂȂ�܂��B
�͈̔͂ɂ����ĂƂ肤��l���l���邱�ƂɂȂ�܂��B 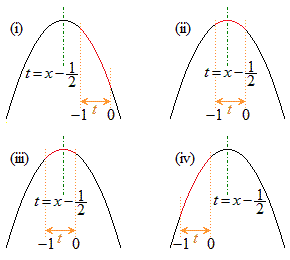
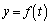 �̃O���t��
�̃O���t��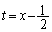 �Ɋւ��đΏ̂Ȃ̂ŁA
�Ɋւ��đΏ̂Ȃ̂ŁA �͈̔͂ɑ��Ď��ʒu
�͈̔͂ɑ��Ď��ʒu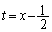 ���ǂ������ʒu�W�ɂ��邩�A�Ƃ������Ƃňȉ���4�ʂ�ɏꍇ�������܂�(�E�}�Q��)�B
���ǂ������ʒu�W�ɂ��邩�A�Ƃ������Ƃňȉ���4�ʂ�ɏꍇ�������܂�(�E�}�Q��)�B(i) 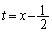 ���͈�
���͈� �̍����ɂ���Ƃ��A
�̍����ɂ���Ƃ��A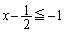 �C�܂�A
�C�܂�A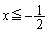
(ii) 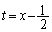 ���͈�
���͈� ���̒��Ԃ��������ɂ���Ƃ��A
���̒��Ԃ��������ɂ���Ƃ��A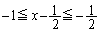 �C�܂�A
�C�܂�A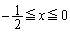
(iii) 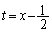 ���͈�
���͈� ���̒��Ԃ����E���ɂ���Ƃ��A
���̒��Ԃ����E���ɂ���Ƃ��A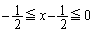 �C�܂�A
�C�܂�A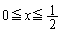
�܂��A�����ł́A�u����PQ�v�̒ʉߔ͈͂ł͂Ȃ��A�u����PQ�v�̒ʉߔ͈͂Ȃ̂ŁA����PQ��̓_��x���W�͈̔�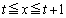 ���l����K�v���o�Ă��܂��B
���l����K�v���o�Ă��܂��B
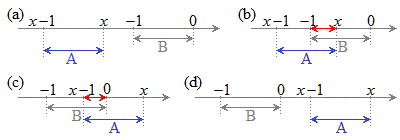
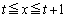 ���At�Ɋւ��āA
���At�Ɋւ��āA �̂ق���
�̂ق���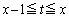 �Ƃ������������̂ŁA
�Ƃ������������̂ŁA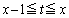 �Ƃ����͈�(�͈�A�Ƃ��܂�)��
�Ƃ����͈�(�͈�A�Ƃ��܂�)�� �Ƃ����͈�(�͈�B�Ƃ��܂�)�̋��ʕ������l���Ȃ�������܂���B
�Ƃ����͈�(�͈�B�Ƃ��܂�)�̋��ʕ������l���Ȃ�������܂���B (a) 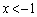 �̂Ƃ��A
�̂Ƃ��A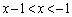 �ƂȂ�̂ŁA�͈�A�Ɣ͈�B�ɂ͋��ʕ����͂���܂���B
�ƂȂ�̂ŁA�͈�A�Ɣ͈�B�ɂ͋��ʕ����͂���܂���B (b) 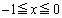 �̂Ƃ��A
�̂Ƃ��A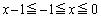 �ƂȂ�̂ŁA�͈�A�Ɣ͈�B�̋��ʕ����́A
�ƂȂ�̂ŁA�͈�A�Ɣ͈�B�̋��ʕ����́A
(c) 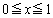 �̂Ƃ��A
�̂Ƃ��A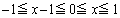 �ƂȂ�̂ŁA�͈�A�Ɣ͈�B�̋��ʕ����́A
�ƂȂ�̂ŁA�͈�A�Ɣ͈�B�̋��ʕ����́A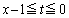
(d) 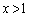 �̂Ƃ��A
�̂Ƃ��A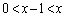 �ƂȂ�̂ŁA�͈�A�Ɣ͈�B�ɂ͋��ʕ����͂���܂���B
�ƂȂ�̂ŁA�͈�A�Ɣ͈�B�ɂ͋��ʕ����͂���܂���B �]���āA(i)�`(iv)��(a)�`(d)�Ƃ���Ax�͈̔͂��A
(�A) 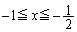 �@((i)����(b))
�@((i)����(b)) (�C) 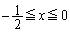 �@((ii)����(b))
�@((ii)����(b)) (�E) 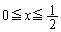 �@((iii)����(c))
�@((iii)����(c)) (�G) 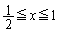 �@((iv)����(c))
�@((iv)����(c)) ��4�͈̔͂ɕ����čl���邱�ƂɂȂ�܂��B
���A�e�ꍇ�ɂ��āA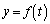 �̂Ƃ蓾��l�͈͈̔͂ȉ��̂悤�ɂȂ�܂�(2�����̍ő�ŏ����Q��)�B
�̂Ƃ蓾��l�͈͈̔͂ȉ��̂悤�ɂȂ�܂�(2�����̍ő�ŏ����Q��)�B (�A) 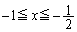 �̂Ƃ��A
�̂Ƃ��A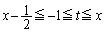 ���A
���A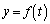 �́A
�́A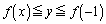 �C�܂�A
�C�܂�A �Ƃ����͈͂̒l���Ƃ�܂��B
(�C) 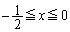 �̂Ƃ��A
�̂Ƃ��A �C
�C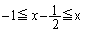 ���A
���A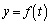 �́A
�́A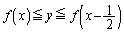 �C�܂�A
�C�܂�A �Ƃ����͈͂̒l���Ƃ�܂��B
(�E) 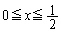 �̂Ƃ��A
�̂Ƃ��A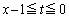 �C
�C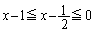 ���A
���A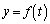 �́A
�́A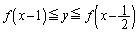 �C�܂�A
�C�܂�A �Ƃ����͈͂̒l���Ƃ�܂��B
(�G) 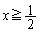 �̂Ƃ��A
�̂Ƃ��A ���A
���A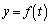 �́A
�́A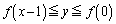 �C�܂�A
�C�܂�A 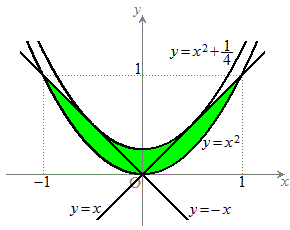 �ȏ�܂Ƃ߂āA����PQ���ʉ߂���̈�́A
�ȏ�܂Ƃ߂āA����PQ���ʉ߂���̈�́A�}������ƁA�E�}���ΐF���F��(���E�����܂�) ......[��]
���D�_P�CQ�͕�����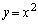 ����_�Ȃ̂ŁA�̈�̋��E���Ƃ���
����_�Ȃ̂ŁA�̈�̋��E���Ƃ���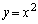 ���o�Ă��܂��B�܂��A������Ƃ��A��L�̂悤�ɂȂ�̂ł����A���������A�ȒP�ɍς܂�������A����PQ�́A����PQ�������
���o�Ă��܂��B�܂��A������Ƃ��A��L�̂悤�ɂȂ�̂ł����A���������A�ȒP�ɍς܂�������A����PQ�́A����PQ�������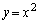 �Ő������Ƃ��̌��ŁA����PQ�̂���
�Ő������Ƃ��̌��ŁA����PQ�̂��� ��������������A�Ƃ��āA(i)�`(iv)�̏ꍇ�킯�݂̂ŁA
��������������A�Ƃ��āA(i)�`(iv)�̏ꍇ�킯�݂̂ŁA �͈̔͂�
�͈̔͂�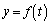 �̂Ƃ蓾��l���A
�̂Ƃ蓾��l���A (i) 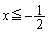 �̂Ƃ��A
�̂Ƃ��A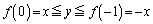
(ii) 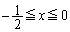 �̂Ƃ��A
�̂Ƃ��A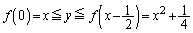
(iii) 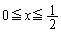 �̂Ƃ��A
�̂Ƃ��A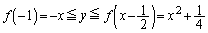
(iv) 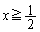 �̂Ƃ��A
�̂Ƃ��A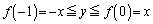
�Ƃ��ċ��߁A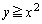 �Ƃ̋��ʕ����A�Ƃ��邱�ƂɂȂ�܂��B
�Ƃ̋��ʕ����A�Ƃ��邱�ƂɂȂ�܂��B �ʉ��D2���������B�F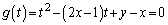 ���l����̂ł���A�B��
���l����̂ł���A�B�� �͈̔͂ɉ������������l���܂�(2���������̈�ʘ_���Q��)�B
�͈̔͂ɉ������������l���܂�(2���������̈�ʘ_���Q��)�B �܂��A�d�����܂߂�2����L����Ƃ��A
(��) ���ʎ��F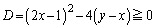
(��) ���F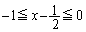
(��) �[�F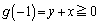 �C
�C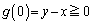
(��)����(��)����(��)���A
 �͈̔͂�1��������L����Ƃ��A
�͈̔͂�1��������L����Ƃ��A�� 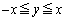 �܂���
�܂���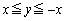 �@����D
�@����D �C�܂��͇D�ł́u����PQ�v�̒ʉߔ͈͂ɂȂ��Ă��܂����߁A��L�̒��D�̂悤�ɂ��āA�u����PQ�v�̒ʉߔ͈͂́A�g�C�܂��͇D�h����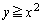 �ł���A�Ƃ��邱�ƂɂȂ�܂��B
�ł���A�Ƃ��邱�ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B