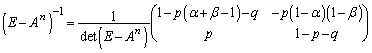�R����㐔�w'09�N[3]
α�Cβ�Ct (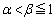 )�������Ƃ���B2�������s��A��
)�������Ƃ���B2�������s��A��
�Ƃ��A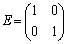 �Ƃ���B���R��n�ɑ��āA
�Ƃ���B���R��n�ɑ��āA
�Ƃ����B
(1) 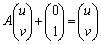 ����
����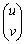 �����߂�B
�����߂�B (2) 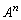 ��n�Cα�Cβ��p����
��n�Cα�Cβ��p����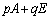 (p�Cq�͎���)�̌`�ɕ\���B
(p�Cq�͎���)�̌`�ɕ\���B (3) 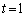 �C
�C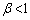 �����藧���A
�����藧���A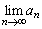 �C
�C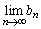 �C
�C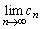 �C
�C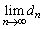 �����݂���Ɖ��肷��B���̂Ƃ��A
�����݂���Ɖ��肷��B���̂Ƃ��A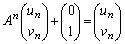 ����
����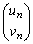 ������1���݂��邱�Ƃ������B����ɁA����
������1���݂��邱�Ƃ������B����ɁA����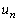 �C
�C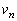 �ɑ���
�ɑ���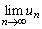 �C
�C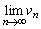 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s���̌v�Z���ʓ|�Ȗ��ł��B(2)�ł́A�n�~���g���E�P�[���[�̒藝�ɂ�鎟�������𗘗p���܂��B
(1) 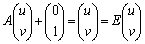
���A
�E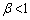 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A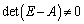 ���
���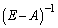 �����݂��܂�(�t�s�����Q��)�B
�����݂��܂�(�t�s�����Q��)�B �@���A
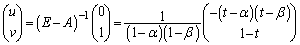 ......[��]
......[��]�E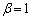 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A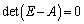 ���
���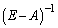 �͑��݂��܂���B
�͑��݂��܂���B �@���A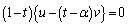 ����
���� 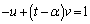
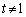 �̂Ƃ��ɂ͑�ӂ��݂���u�Cv�͑��݂��܂���B
�̂Ƃ��ɂ͑�ӂ��݂���u�Cv�͑��݂��܂���B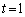 �̂Ƃ��A
�̂Ƃ��A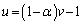
����āAw��C�ӂ̎����Ƃ��āA
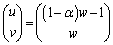 ......[��]
......[��]
(2) 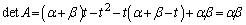
���ӂ�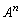 �������āA
�������āA 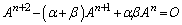 �@����A
�@����A�ƕό`����̂Ɠ��l�̎��ό`���s���܂��B
�A �� 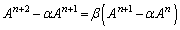
������A
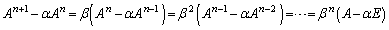 �@����B
�@����B���l�ɁA
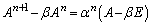 �@����C
�@����C�B�|�C���A
�� 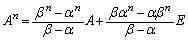 ......[��]�@����D
......[��]�@����D
�܂�A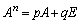 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A 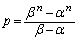 �C
�C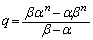 �@����E
�@����E
(3) 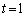 �̂Ƃ��A
�̂Ƃ��A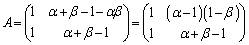
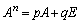 ���A
���A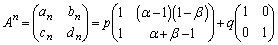
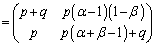 �@����F
�@����F������A
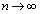 �̂Ƃ�
�̂Ƃ�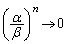 �@(���䐔��̋Ɍ����Q��)
�@(���䐔��̋Ɍ����Q��)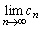 �����݂���̂ŁA
�����݂���̂ŁA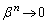 �C
�C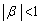 �@(
�@(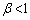 �ɒ���)
�ɒ���)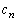 �̌`������ƁAα�ɂ��Ă�
�̌`������ƁAα�ɂ��Ă�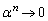 ��
��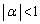
�E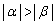 �̂Ƃ��A
�̂Ƃ��A 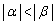 �C
�C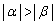 ������ɂ��Ă��A
������ɂ��Ă��A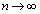 �̂Ƃ�
�̂Ƃ�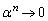 �C
�C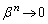 ��
��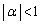 �C
�C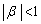 �@����G
�@����G���A
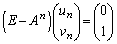 �@����H
�@����H�F���A
�E��p���āA
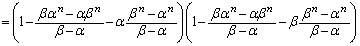
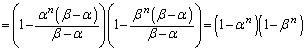 �@����I
�@����I�G���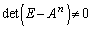 �C����āA
�C����āA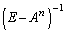 �����݂��܂��B
�����݂��܂��B
�H���A 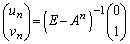 �@����J
�@����J������A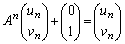 ����
����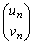 ������1���݂��܂��B
������1���݂��܂��B
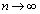 �̂Ƃ��A�E�C�G���A
�̂Ƃ��A�E�C�G���A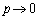 �C
�C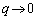
�G�C�I���A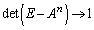
����āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 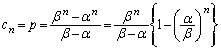
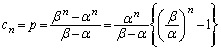
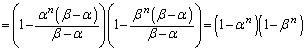 �@����I
�@����I