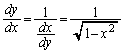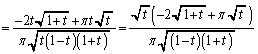�����吔�w'10�N[3]
��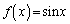 (
(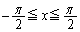 )�̋t����
)�̋t����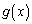 (
(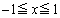 )�Ƃ����Ƃ��A���̖₢�ɓ�����B
)�Ƃ����Ƃ��A���̖₢�ɓ�����B
��1�@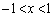 �̂Ƃ��A
�̂Ƃ��A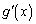 ��x��p���ĕ\���B
��x��p���ĕ\���B ��2�@�Ȑ�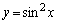 (
(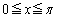 )�ƒ���
)�ƒ���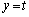 (
(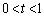 )��2�̌�_��x���W���A���ꂼ��α�Cβ (
)��2�̌�_��x���W���A���ꂼ��α�Cβ (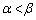 )�Ƃ����Ƃ��A
)�Ƃ����Ƃ��A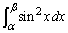 ��t �Ɗ�g��p���ĕ\���B
��t �Ɗ�g��p���ĕ\���B ��3�@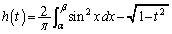 (
(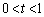 )�Ƃ����Ƃ��A
)�Ƃ����Ƃ��A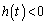 (
(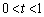 )�������A
)�������A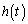 ���ŏ��ɂ���t �̒l�����߂�B
���ŏ��ɂ���t �̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʓ|�Ȕ��ς̌v�Z���ł��B��������₱�����̂Œ��ӂ��Ă��������B
��1�@��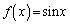 (
(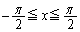 )�̋t����
)�̋t����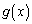 (
(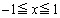 )�ł���Ƃ��A
)�ł���Ƃ��A 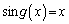 �@����@
�@����@�����ŁA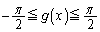 �ł��B�܂��A
�ł��B�܂��A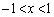 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A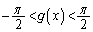 �ƂȂ�܂��B
�ƂȂ�܂��B
���ӂ�x�Ŕ������āA 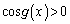 �Ƈ@���A
�Ƈ@���A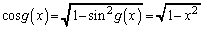 �C����āA
�C����āA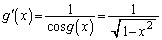 ......[��]
......[��]
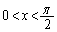 �ł͑������A
�ł͑������A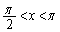 �ł͌������ł��B
�ł͌������ł��B
�Ȑ�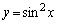 �ƒ���
�ƒ���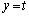 ��2�̌�_��x���Wα�Cβ �ɂ��āA
��2�̌�_��x���Wα�Cβ �ɂ��āA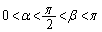 �ƂȂ��Ă��܂��B
�ƂȂ��Ă��܂��B
�]���āA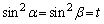 �C
�C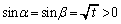 �C
�C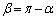 �C
�C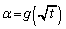 �C
�C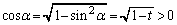 �C
�C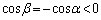 �ł��B������p���āA
�ł��B������p���āA
��3�@��2�̌��ʂ�p���āA
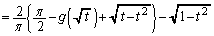
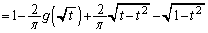 �@����A
�@����A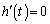 �Ƃ���ƁA
�Ƃ���ƁA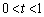 �ɂ����ẮA
�ɂ����ẮA�� 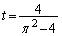 �@(
�@(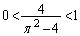 )�@�ɂ����āA
)�@�ɂ����āA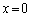 �Ƃ����
�Ƃ����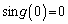 �C
�C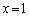 �Ƃ����
�Ƃ����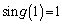
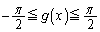 ���l������ƁA
���l������ƁA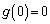 �C
�C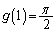
����āA�A���A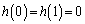
�����\�͈ȉ��̂悤�ɂȂ�܂�(���̑������Q��)�B�����\���A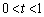 �ɂ�����
�ɂ�����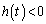
�܂��A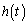 ���ŏ��ɂ���t�́A
���ŏ��ɂ���t�́A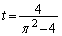 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B