�d�ʑ吔�w'10�N���[4]
��PCD�̕�PC�̒��_��A�C��PD�̒��_��B�C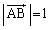 �Ƃ���B
�Ƃ���B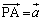 �C
�C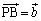 �C
�C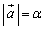 �C
�C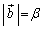 �Ƃ��āA����AB��α�Fβ �ɓ�������_��Q�C����CB��α�F1�ɓ�������_��R�C����PQ�ƒ���AR�̌�_��E�Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ��āA����AB��α�Fβ �ɓ�������_��Q�C����CB��α�F1�ɓ�������_��R�C����PQ�ƒ���AR�̌�_��E�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) 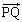 ��
��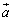 �C
�C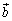 �Cα�Cβ ��p���ĕ\���B
�Cα�Cβ ��p���ĕ\���B (3) 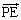 ��
��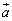 �C
�C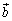 �Cα�Cβ ��p���ĕ\���B
�Cα�Cβ ��p���ĕ\���B (4) �_E������CD��ɂ���Ƃ��Aα�Cβ �̖������W�������߂�B
(5) ��AB���Œ肵�āA�_P��(4)�ŋ��߂��W�������Ȃ��瓮���Ƃ��A��PAB�̖ʐς̍ő�lS�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ʃx�N�g���̊�{���ł����A(5)�ŁAP���O�����ȉ~�ł��B
(2) 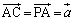 �C
�C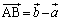 ���A
���A 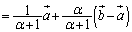
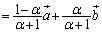 ......[��]
......[��]
(3) 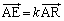 �Ƃ����ƁA(2)�̌��ʂ�p���āA
�Ƃ����ƁA(2)�̌��ʂ�p���āA 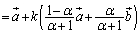
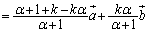 �@����@
�@����@����A(1)�̌��ʂ�p���āA
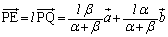 �@����A
�@����A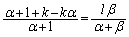 �@����B
�@����B
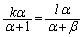 �@����C
�@����C�C���A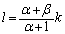
�B�ɑ�����āA 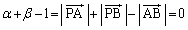 �̂Ƃ��AP�͐���AB��ɗ��āA��PCD���ł��Ȃ��̂ŁA
�̂Ƃ��AP�͐���AB��ɗ��āA��PCD���ł��Ȃ��̂ŁA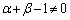 ���A
���A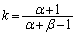 �C
�C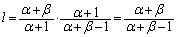
�A���A
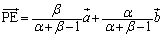 ......[��]
......[��]
(4) 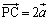 �C
�C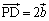 ���A
���A �_E������CD��ɂ���Ƃ��A
�� 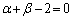 ......[��]
......[��]
(5) (4)�̌��ʂ��A�_P��2��_A�CB�Ƃ̋����̘a��2�Ȃ̂ŁA�_P�́AA�CB��2�œ_�Ƃ��A�����̒�����2�ƂȂ�ȉ~��̓_�ł��B
���̑ȉ~�̏œ_�ԋ�����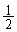 ��
��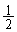 �C��������1�C���Z���́A
�C��������1�C���Z���́A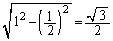
��PAB�̒�ӂ�1�C���������Z���ɂȂ�Ƃ�(���̂Ƃ��A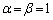 )�ɁA��PAB�̖ʐύő�ŁA�ő�lS�́A
)�ɁA��PAB�̖ʐύő�ŁA�ő�lS�́A 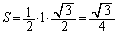 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B