��吔�w'10�N[6]
�ȉ~O�F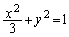 �C����l�F
�C����l�F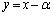 (
(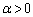 )�C����
)�C����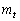 �F
�F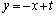 ������B�ȉ~O�ƒ���l���ڂ��Ă���Ƃ��A���̖₢�ɓ�����B
������B�ȉ~O�ƒ���l���ڂ��Ă���Ƃ��A���̖₢�ɓ�����B
(1) α�̒l�����߂�B�܂��A�ȉ~O�ƒ���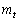 ��2�̋��L�_�����悤�ɁAt�̒l�̑��ݔ͈͂����߂�B
��2�̋��L�_�����悤�ɁAt�̒l�̑��ݔ͈͂����߂�B (2) ����l�ƒ���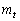 �̌�_��_H�Ƃ���Ƃ��A�_A
�̌�_��_H�Ƃ���Ƃ��A�_A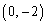 �Ɠ_H�Ƃ̋���s��t��p���ĕ\���B�܂��A�ȉ~O�ƒ���
�Ɠ_H�Ƃ̋���s��t��p���ĕ\���B�܂��A�ȉ~O�ƒ���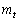 ��2�̋��L�_P�CQ�����Ƃ��A
��2�̋��L�_P�CQ�����Ƃ��A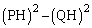 ��t��p���ĕ\���B�������A
��t��p���ĕ\���B�������A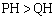 �Ƃ���B
�Ƃ���B (3) �ȉ~O��l�̂܂���1��]���Ăł����]�̂̑̐�V�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ή�]���̑̐ς̖��ł����A�ȉ~���߂ɉ�]�����Ă݂悤�A�Ƃ����킯�ŁA���낢��ƍH�v���K�v�ɂȂ�܂��B�Ă��˂��ȗU���ɉ����Đi�߂čs���܂��B
�ȉ~O�F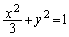 �@����@
�@����@
����l�F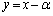 �@����A
�@����A
����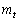 �F
�F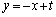 �@����B
�@����B
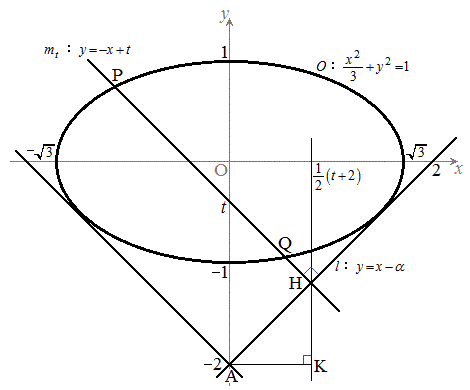 (1) �@�ƇA��A������ƁA
(1) �@�ƇA��A������ƁA�ȉ~O�ƒ���l���ڂ���̂ŁA����2���������͏d���������܂��B���ʎ�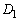 �ɂ��āA
�ɂ��āA 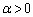 ���A
���A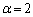 ......[��]������A����l�F
......[��]������A����l�F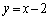 �@����C
�@����C
�@�ƇB��A������ƁA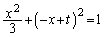
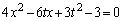 �@����D
�@����D�ȉ~O�ƒ���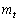 ��2�̋��L�_�����̂ŁA����2����������2�̑��قȂ�������������܂��B���ʎ�
��2�̋��L�_�����̂ŁA����2����������2�̑��قȂ�������������܂��B���ʎ�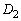 �ɂ��āA
�ɂ��āA �� 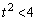 ��
�� 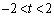 ......[��]
......[��]
(2) �B�ƇC��A������ƁA
�� 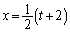 (
(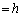 �Ƃ����܂�)�@����E
�Ƃ����܂�)�@����E
���ꂪ�_H��x���W�ł��B�_A����A�����F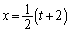 �ɐ���AK�����낷�ƁA����l�̌X����1�ł��邱�Ƃ���A���p�O�p�`AHK�͒��p�ӎO�p�`�ŁAAK�FAH = 1�F
�ɐ���AK�����낷�ƁA����l�̌X����1�ł��邱�Ƃ���A���p�O�p�`AHK�͒��p�ӎO�p�`�ŁAAK�FAH = 1�F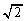 ���A
���A 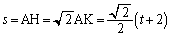 �@����F
�@����F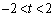 �̉��ŁA�D��2����p�Cq (
�̉��ŁA�D��2����p�Cq (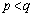 )�Ƃ���ƁA
)�Ƃ���ƁA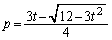 �C
�C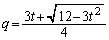
�_P�C�_Q��x���W��p�Cq�ł��B
����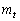 �̌X����
�̌X����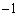 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A
(3) �f�ʐς�l�ɉ����Đϕ�����Ηǂ��킯�ł����A����l�ɉ����č��W���Ƃ�A����l�Ɛ����ȕ��ʂʼn�]�̂�����Ƃ��̒f�ʐς��l���܂��B
AH�̒���s��l�ɉ����ĂƂ������W�Ƃ��܂��B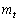 ��l�������Ȃ̂ŁA�f�ʐς́A�O���̉~�̖ʐ�
��l�������Ȃ̂ŁA�f�ʐς́A�O���̉~�̖ʐ� ��������̉~�̖ʐ�
��������̉~�̖ʐ� �����������̂ɂȂ�܂��B
�����������̂ɂȂ�܂��B 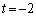 �̂Ƃ��A�_H��x���W��0��
�̂Ƃ��A�_H��x���W��0��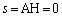 �C
�C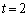 �̂Ƃ��A�_H��x���W��2��
�̂Ƃ��A�_H��x���W��2��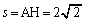
t�� �͈̔͂��܂����A���̂Ƃ��A
�͈̔͂��܂����A���̂Ƃ��A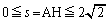
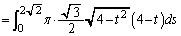 �@(�� (2))
�@(�� (2))�F��p�����u���ϕ������܂��B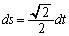 �Cs�F
�Cs�F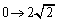 �̂Ƃ�t�F
�̂Ƃ�t�F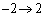
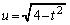 �Ƃ����ƁA
�Ƃ����ƁA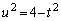 �C
�C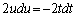 �C
�C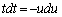 �Ct�F
�Ct�F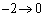 �̂Ƃ�u�F
�̂Ƃ�u�F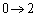 �Ct�F
�Ct�F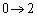 �̂Ƃ�u�F
�̂Ƃ�u�F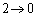
�ȏ���A
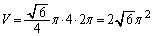 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B