�k�嗝�n���w'10�N���[1]
���̘A���s�����̕\���̈��D�Ƃ���B
(1) �̈�D��}������B
(2) �_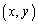 �����̗̈�D���Ƃ��A
�����̗̈�D���Ƃ��A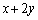 �̍ő�lM�ƍŏ��lm�����߂�B�܂��AM�Cm��^����D�̓_�����߂�B
�̍ő�lM�ƍŏ��lm�����߂�B�܂��AM�Cm��^����D�̓_�����߂�B (3) a�������Ƃ���B�_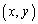 ���̈�D���Ƃ��A
���̈�D���Ƃ��A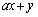 ���_
���_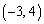 �ōő�l���Ƃ�悤��a�͈̔͂����߂�B
�ōő�l���Ƃ�悤��a�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���`�v��@�̖��ł��B
 (1) �̈�D�̋��E���́A
(1) �̈�D�̋��E���́A�@�C�A��A������ƁA
�������āA
�� 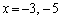
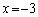 �̂Ƃ�
�̂Ƃ�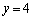 �C
�C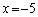 �̂Ƃ�
�̂Ƃ�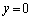
�@�C�B��A������ƁA �� 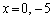
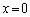 �̂Ƃ�
�̂Ƃ�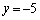 �C
�C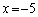 �̂Ƃ�
�̂Ƃ�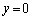
�@�C�A�C�B��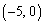 �Ō����܂��B�̈�D�͉~�@��������ŁA
�Ō����܂��B�̈�D�͉~�@��������ŁA
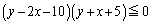 �ɂ����āA
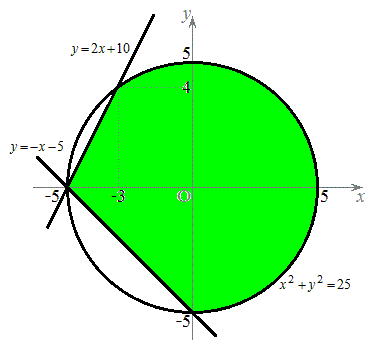
�ɂ����āA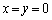 �Ƃ���Ɛ��藧�̂ŁA3�̋��E���ň͂�ꂽ�̈�̂����A���_���܂ޕ����ŁA�}������ƁA�E�}���ΐF���F��(���E�����܂�)�B
�Ƃ���Ɛ��藧�̂ŁA3�̋��E���ň͂�ꂽ�̈�̂����A���_���܂ޕ����ŁA�}������ƁA�E�}���ΐF���F��(���E�����܂�)�B
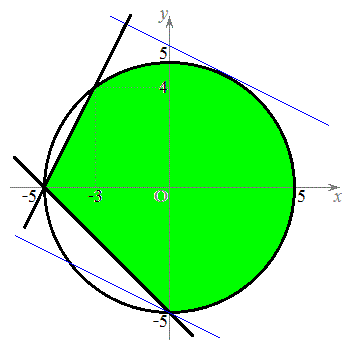 (2)
(2) 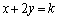 �@����C
�@����C�Ƃ����ƁA�X��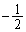 �Cy�ؕ�k�̒�����\���܂��B�_
�Cy�ؕ�k�̒�����\���܂��B�_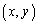 ��(1)�Ő}�������̈�D���̂ŁA�����C�͗̈�D�Ƌ��L�_�������Ȃ���Ȃ�܂���B�����Ȃ�̂́A
��(1)�Ő}�������̈�D���̂ŁA�����C�͗̈�D�Ƌ��L�_�������Ȃ���Ȃ�܂���B�����Ȃ�̂́A (i) �����C���~��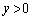 �̕����Őڂ���Ƃ���k�̒l
�̕����Őڂ���Ƃ���k�̒l ����A
(ii) �����C���_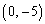 ��ʂ�Ƃ���k�̒l
��ʂ�Ƃ���k�̒l �܂ł̊Ԃ̒l���Ak���Ƃ�Ƃ��ł��B
(i)�́A�@�ƇC��A�����āA
�������āA
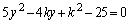 �@����D
�@����D�@�ƇC�͐ڂ���̂ŁA����2���������͏d���������܂��B
�� 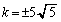 ���̂Ƃ��D�́A
���̂Ƃ��D�́A 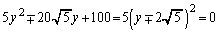 �@(��������)
�@(��������)(ii)�́A�C��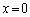 �C
�C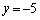 �������āA
�������āA (i)�C(ii)���A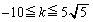
�����̕s�����̓����́A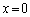 �C
�C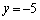 �̂Ƃ��A�E���̕s�����̓����́A
�̂Ƃ��A�E���̕s�����̓����́A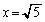 �C
�C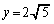 �̂Ƃ��ɐ������܂��B�ȏ���A
�̂Ƃ��ɐ������܂��B�ȏ���A
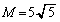 �C�����^����D�̓_��
�C�����^����D�̓_��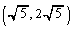 �C
�C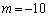 �C�����^����D�̓_��
�C�����^����D�̓_��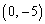 ......[��]
......[��]
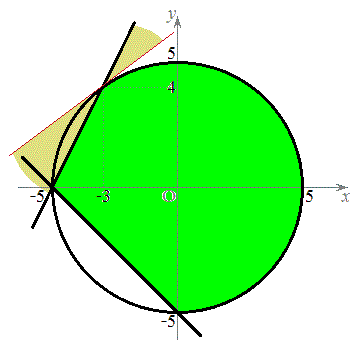 (3)
(3) 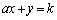 �@����E
�@����E�Ƃ����ƁA�X��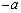 �Cy�ؕ�k�̒�����\���܂��B�_
�Cy�ؕ�k�̒�����\���܂��B�_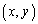 ���̈�D���̂ŁA(2)�Ɠ��l�A�����E�͗̈�D�Ƌ��L�_�������܂��B
���̈�D���̂ŁA(2)�Ɠ��l�A�����E�͗̈�D�Ƌ��L�_�������܂��B
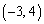 ��k���ő�l���Ƃ�̂ŁAk���ő�l���Ƃ�Ƃ��A�����E��
��k���ő�l���Ƃ�̂ŁAk���ő�l���Ƃ�Ƃ��A�����E��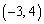 ��ʂ�A
��ʂ�A 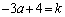 �@����F
�@����F���̂Ƃ��A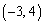 ��ʂ钼�����̈�D��2�̗̈�ɕ�����悤�Ȓ����ł���Ɖ��肷��ƁA2�̗̈�̂����ꂩ����̗̈���̓_��ʂ蒼���E�ƕ��s�Ȓ���(�X��
��ʂ钼�����̈�D��2�̗̈�ɕ�����悤�Ȓ����ł���Ɖ��肷��ƁA2�̗̈�̂����ꂩ����̗̈���̓_��ʂ蒼���E�ƕ��s�Ȓ���(�X��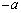 )��y�ؕЂ�k�����傫���Ȃ�܂��B�Ƃ������Ƃ́A
)��y�ؕЂ�k�����傫���Ȃ�܂��B�Ƃ������Ƃ́A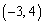 ��k�ő��^����_�ł͂Ȃ��A�Ƃ������ƂɂȂ薵�����܂��B�܂�Ak�̍ő�l��^���钼���E���̈�D��2�̗̈�ɕ����邱�Ƃ͂���܂���B
��k�ő��^����_�ł͂Ȃ��A�Ƃ������ƂɂȂ薵�����܂��B�܂�Ak�̍ő�l��^���钼���E���̈�D��2�̗̈�ɕ����邱�Ƃ͂���܂���B
�Ƃ������Ƃ́A�����E�̌X���́A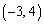 �ɂ����ĉ~�@�Ɛڂ��钼���̌X���ƁA�����A�̌X��2�܂ł̊Ԃ̒l���Ƃ�Ƃ������Ƃł��B
�ɂ����ĉ~�@�Ɛڂ��钼���̌X���ƁA�����A�̌X��2�܂ł̊Ԃ̒l���Ƃ�Ƃ������Ƃł��B
�����E��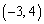 �ɂ����ĉ~�@�Ɛڂ���Ƃ��A
�ɂ����ĉ~�@�Ɛڂ���Ƃ��A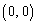 �ƒ����E�Ƃ̋�����5�ƂȂ�(�~�ƒ����̈ʒu�W���Q��)�A
�ƒ����E�Ƃ̋�����5�ƂȂ�(�~�ƒ����̈ʒu�W���Q��)�A ����ƇF���A
�� 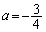 �@(�����E�̌X����
�@(�����E�̌X����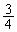 )
) �� 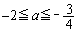 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B