広島大理系数学'10年後期[3]
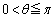 に対して
に対して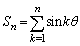 (
( )を考える。以下の問いに答えよ。
)を考える。以下の問いに答えよ。
(1) 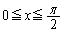 のとき、
のとき、 が成り立つことを示せ。
が成り立つことを示せ。 (2) 等式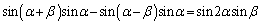 を示せ。
を示せ。 (3)  が成り立つことを示せ。
が成り立つことを示せ。 (4)  が成り立つことを示せ。
が成り立つことを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 不等式の証明が付属していますが、三角関数で表される数列の和を求めよう、という問題です。
(1)  のグラフと
のグラフと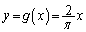 のグラフを考えます。
のグラフを考えます。 より、両グラフとも、2点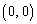 ,
,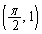 を通ります。
を通ります。
 において、
において、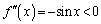 より、
より、 のグラフは上に凸です(関数の凹凸を参照)。
のグラフは上に凸です(関数の凹凸を参照)。
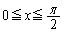 において、
において、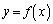 のグラフは両端を除いて、両端を結ぶ直線
のグラフは両端を除いて、両端を結ぶ直線 のグラフより上にあります。よって、
のグラフより上にあります。よって、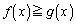 ,即ち、
,即ち、
(2) 
(3) (2)をどう使うか、ということを考えることになりますが、示すべき不等式の分母を払うと、
となるので、Σ内の式と、(2)の右辺とを見比べて、
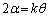 ,
,
とおきます。(2)を用いて、
つまり、
これを、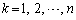 について、加え合わせると、左辺は、
について、加え合わせると、左辺は、 となり、右辺は、
(4) (3)で示した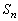 の式では、右辺の派手な分子に目が行きがちですが、
の式では、右辺の派手な分子に目が行きがちですが、 ,
,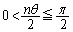 とは言えないので(1)が利用できません。目立たないですが、分母の
とは言えないので(1)が利用できません。目立たないですが、分母の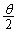 の方に着目します。
の方に着目します。 より、
追記.(3)の等式は、ド・モアブルの定理を使うと、等比数列の和の公式を用いて証明できます。ド・モアブルの定理より、iを虚数単位、nを整数として、 ∴  実部、虚部を比較して、
実部、虚部を比較して、  ,
,
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  が成り立つことを示せ。
が成り立つことを示せ。
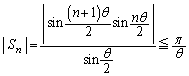
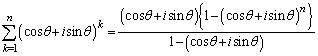




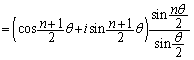

 ,
,