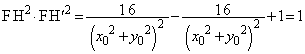�������吔�w'10�N[6]
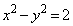 �ŕ\�����Ȑ���C�Ƃ��AP
�ŕ\�����Ȑ���C�Ƃ��AP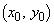 ��C��̓_�Ƃ���B���̊e�₢�ɓ�����B
��C��̓_�Ƃ���B���̊e�₢�ɓ�����B
(1) �Ȑ�C��̓_P�ɂ�����ڐ�l�̕������́A
�ƂȂ邱�Ƃ��ؖ�����B
(2) ���_O����l�ɂ��낵��������OH�Ƃ���BH�̍��W��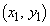 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A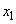 �C
�C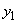 ��
��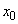 �C
�C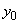 �ŕ\���B
�ŕ\���B (3) F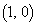 �C
�C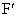
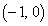 �Ƃ���B
�Ƃ���B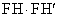 �͓_P�̎����ɂ�炸���ł��邱�Ƃ��ؖ�����B�܂��A���̒l�����߂�B
�͓_P�̎����ɂ�炸���ł��邱�Ƃ��ؖ�����B�܂��A���̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�o�Ȑ����e�[�}�Ƃ���v�Z���ł����A���Ɍv�Z���Ȃ��ƍs���l�܂�܂��B
(1) C�F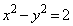 �@����@
�@����@ 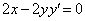 �@����A
�@����A(i) 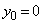 �̂Ƃ��A
�̂Ƃ��A �@��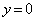 �Ƃ����
�Ƃ����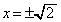
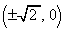 �ɂ�����C�̐ڐ�l�́A
�ɂ�����C�̐ڐ�l�́A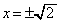 (��������)�@����B
(��������)�@����B (ii) 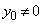 �̂Ƃ��A
�̂Ƃ��A �A��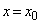 �C
�C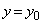 �Ƃ���A
�Ƃ���A 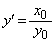 �@����C
�@����C���ꂪ�AP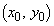 �ɂ�����C�̐ڐ�l�̌X���ł��B�ڐ�l�̕������́A
�ɂ�����C�̐ڐ�l�̌X���ł��B�ڐ�l�̕������́A P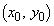 ��C��̓_�Ň@�����̂ŁA
��C��̓_�Ň@�����̂ŁA 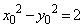 �@����D
�@����D����āA�ڐ�l�́A
�����ŁA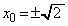 �C
�C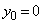 �Ƃ���ƁA�B���܂�ł��܂��B
�Ƃ���ƁA�B���܂�ł��܂��B �ȏ���A�Ȑ�C��̓_P�ɂ�����ڐ�l�̕������́A
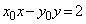 �@����E
�@����E�ƂȂ�܂��B
(2) �Ȑ�C�̐ڐ��ŁAy��(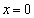 )�Ɛ����ɂȂ���̂͂Ȃ��̂ŁA�ڐ�l�Ɛ����Ȓ���OH�̌X���́A�C���A
)�Ɛ����ɂȂ���̂͂Ȃ��̂ŁA�ڐ�l�Ɛ����Ȓ���OH�̌X���́A�C���A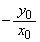 (
(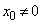 )�@(�����̕��s�Ɛ������Q��)
)�@(�����̕��s�Ɛ������Q��) ����OH�́A
�E�ƘA������ƁA
(3) 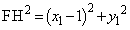
�����ŁA(2)�̌��ʂ�p���āA
����āA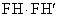 �͓_P�̎����ɂ�炸���ŁA���̒l��1 ......[��]�@�ł��B
�͓_P�̎����ɂ�炸���ŁA���̒l��1 ......[��]�@�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 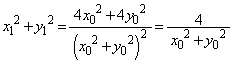
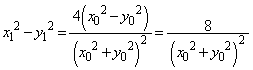 �@(�� �D)
�@(�� �D)