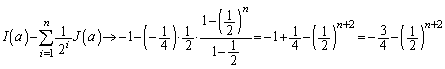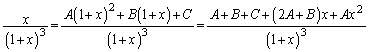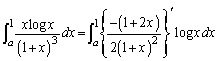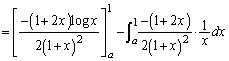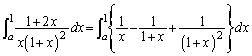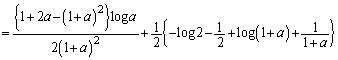�ޗnj�����吔�w'10�N[4]
n�𐳐����Ƃ���B
(1) 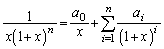 �ƂȂ�萔
�ƂȂ�萔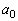 �C
�C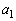 �C����C
�C����C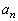 �����߂�B
�����߂�B (2) �����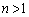 �Ƃ���B1��菬�������̎���a��0�ɋ߂Â��Ƃ��A�Ɍ�
�Ƃ���B1��菬�������̎���a��0�ɋ߂Â��Ƃ��A�Ɍ�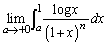 �́A����������̖�����ɂ����U�����A�L���̒l���Ƃ邱�Ƃ��ؖ�����B(�A���A�Ɍ��l����̓I�ɋ��߂�K�v�͂Ȃ��B�܂��A
�́A����������̖�����ɂ����U�����A�L���̒l���Ƃ邱�Ƃ��ؖ�����B(�A���A�Ɍ��l����̓I�ɋ��߂�K�v�͂Ȃ��B�܂��A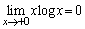 �ł��邱�Ƃ͏ؖ��Ȃ��ɗp���Ă悢)
�ł��邱�Ƃ͏ؖ��Ȃ��ɗp���Ă悢) (3) �Ɍ��l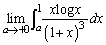 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���������������e�[�}�Ƃ������ł��B(2)�́A��̓I�Ȓl�����߂�K�v�͂Ȃ��A�Ƃ����q���g����A�͂��݂��������p���čl���܂��B
(1) ��C�ɕЕt����̂͑�ςȂ̂ŁA�������Ă����܂��B
�Ƃ����ƁA
������A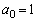 �C
�C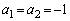
�� 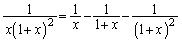
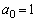 �C
�C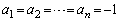 �ɂȂ肻���Ȃ̂ŁAn��1�ω������Ƃ��̈Ⴂ�ׂĂ݂܂��B
�ɂȂ肻���Ȃ̂ŁAn��1�ω������Ƃ��̈Ⴂ�ׂĂ݂܂��B
�ƂȂ�萔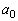 �C
�C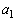 �C����C
�C����C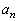 ���A
���A
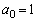 �C
�C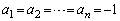 �ł��邱�Ƃ𐔊w�I�A�[�@�ɂ�莦���B
�ł��邱�Ƃ𐔊w�I�A�[�@�ɂ�莦���B ����āA���藧�B
(�U) 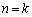 �̂Ƃ��A
�̂Ƃ��A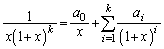 �ƂȂ�萔
�ƂȂ�萔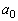 �C
�C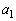 �C����C
�C����C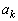 ���A
���A 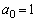 �C
�C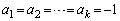
���Ɖ��肷��B
���ӂ�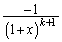 �������āA
�������āA ���ӂ́A
�ƂȂ�A
����āA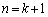 �̂Ƃ������藧�B
�̂Ƃ������藧�B (�T)�C(�U)���A
�ƂȂ�萔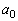 �C
�C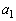 �C����C
�C����C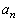 �́A
�́A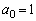 �C
�C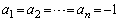 ......[��]
......[��]
(2) (1)���A
���ӂ�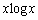 �������āA
�������āA 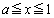 �͈̔͂Őϕ�����ƁA
�͈̔͂Őϕ�����ƁA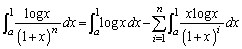 �@����A
�@����A
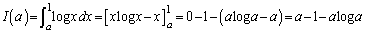 �@����B
�@����B����āA�C���A
����ƇA�C�B���A
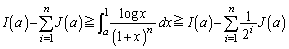 �@����D
�@����D�����ŁA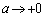 �Ƃ���ƁA
�Ƃ���ƁA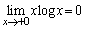 ���A
���A �]���āA
�D�ɂ����āA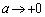 �̂Ƃ��A���ӂ��E�ӂ�����L���m��l�Ɏ�������̂ŁA���ӂ�
�̂Ƃ��A���ӂ��E�ӂ�����L���m��l�Ɏ�������̂ŁA���ӂ�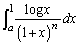 ���L���m��l�Ɏ������܂�(���ӂƉE�ӂ��قȂ�l�Ɏ�������̂ŁA
���L���m��l�Ɏ������܂�(���ӂƉE�ӂ��قȂ�l�Ɏ�������̂ŁA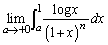 �̒l�͂킩��܂���)�B
�̒l�͂킩��܂���)�B
(3) (2)��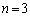 �̏ꍇ���ƈ�u�v���܂����A��ϕ�����x���������Ă���̂ŁA(2)�����p�ł���킯�ł͂���܂���B�]���āA
�̏ꍇ���ƈ�u�v���܂����A��ϕ�����x���������Ă���̂ŁA(2)�����p�ł���킯�ł͂���܂���B�]���āA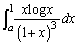 ���ǂ�����Đϕ����邩���l���Ȃ�������܂���B��ϕ����́Ax�̕��������ΐ����̐ςɂȂ��Ă��܂����Ax�̕������̕�����
���ǂ�����Đϕ����邩���l���Ȃ�������܂���B��ϕ����́Ax�̕��������ΐ����̐ςɂȂ��Ă��܂����Ax�̕������̕�����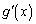 �̌`�ɂȂ�Ȃ����A�ƁA�l���Ă݂܂��B�܂�A
�̌`�ɂȂ�Ȃ����A�ƁA�l���Ă݂܂��B�܂�A 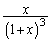 �������ɕ����邽�߂ɁA
�������ɕ����邽�߂ɁA�Ƃ����ƁA
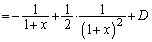
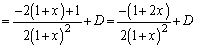 �@(D�F�ϕ��萔)
�@(D�F�ϕ��萔)��2���̒�ϕ��́A�ĂсA���������ɕ����邽�߂ɁA�@�ɂ����āA
�ȏ���A
�����ŁA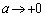 �Ƃ���ƁA
�Ƃ���ƁA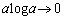 ���A
���A �� 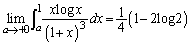 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 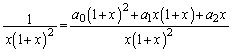
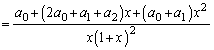 �@����@
�@����@