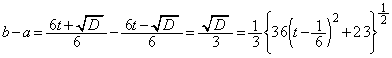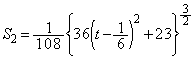帯広畜産大数学'10年[2]
関数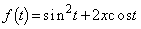
のtに関する最大値
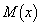をxの関数とする。
(1) 
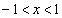のとき、
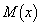をxを用いて表し、曲線
の概形を描け。 (2) 曲線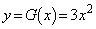
と
で囲まれる図形の面積を求めよ。 (3) 直線
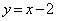上の点Qから、曲線
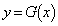に引いた2本の接線
，
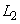の接点のx座標をそれぞれa，bとする。点Qの座標をa，bを用いて表せ。 (4) 2本の接線
，
と曲線
で囲まれる図形の面積の最小値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 2次関数の最大最小がからみますが、数学Ⅱの範囲の微積の総合問題です。
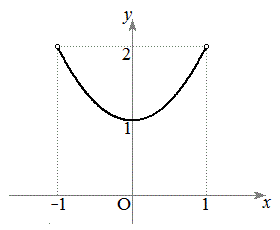(1) 
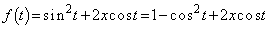
......[答]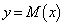 
を図示すると右図実線(白マルを除く)。
(2) 
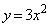と
を連立して、 
∴ 
......[答]
(3) 接点のx座標をpとします。
，
∴ 
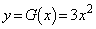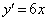
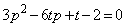･･･② 判別式：
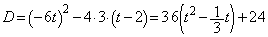
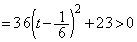･･･③よって、pに関する2次方程式②は、相異なる2解を持ちます。この2解がa，bです。解と係数の関係より、 点Qの座標は、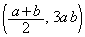
......[答] (
と書くこともできます)
(4) 
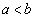とします。①において、
，
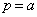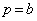として、2本の接線
，
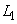は、 2本の接線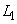
，
と曲線
で囲まれる図形を直線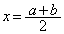
で分けて面積を考えることにより、この図形の面積
は、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。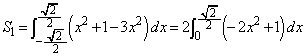 
，
より、
は
のとき最大値
をとります。
，
∴ 
，
(
)
：
，
：
は
のとき、最小値：
......[答] をとります。
において
より、
･･･①
上の点
