�啪��㐔�w'10�N[3]
�����\�Ȋ�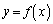 �����̕����������Ƃ���B
�����̕����������Ƃ���B
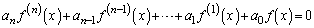 �@���(A)
�@���(A)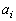 (
(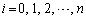 )�͎����̒萔�ŁA
)�͎����̒萔�ŁA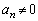 �ł���B�܂��A
�ł���B�܂��A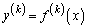 ��
��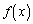 ��k��������
��k��������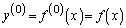 �Ƃ���B(A)�̂悤�ȕ��������n�K�����������Ƃ����A(A)�ɑ���t��n��������
�Ƃ���B(A)�̂悤�ȕ��������n�K�����������Ƃ����A(A)�ɑ���t��n��������
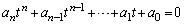 �@���(B)
�@���(B)
(1) ����������(B)�̉�������r�ł���Ƃ��A��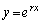 ��������(A)�������Ƃ��ؖ�����B
��������(A)�������Ƃ��ؖ�����B (2) n��������(B)������r��k�d���ɂ��Ƃ��A����t�Ɋւ����������r��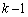 �d���ɂ����Ƃ��ؖ�����B�������A
�d���ɂ����Ƃ��ؖ�����B�������A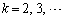 �Ƃ���B
�Ƃ���B (��)�@t��m�����������K���ȑ�����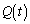 ��p����
��p����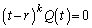 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A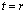 �����̕�������k�d���ƒ�`����B�������A
�����̕�������k�d���ƒ�`����B�������A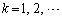 �Ƃ���B
�Ƃ���B (3) �����̒萔r�ɑ���x�̊���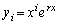 (
(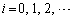 )�Ƃ���B���̂Ƃ��A
)�Ƃ���B���̂Ƃ��A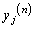 ��x�C
��x�C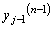 �����
�����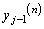 ��p���ĕ\���B�������A
��p���ĕ\���B�������A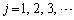 �Ƃ���B
�Ƃ���B (4) ����r��n��������(B)��k�d���ł���Ƃ��A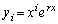 (
(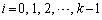 )������������(A)�������Ƃ��ؖ�����B�������Ak�͎��R���Ƃ���B
)������������(A)�������Ƃ��ؖ�����B�������Ak�͎��R���Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���`�������������l�^�Ƃ����S�I�Ȗ��ł��B
(1) ����������(B)�̉�������r�ł���Ƃ��A
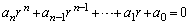 �@����@
�@����@
(2) n��������(B)������r��k�d���ɂ��Ƃ��A�K���ȑ�����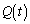 ��p���āA
��p���āA 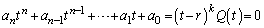 �@����A
�@����A����āA
���̗��ӂ�t�Ŕ�������ƁA
���̂Ƃ��A
���A������
�́Ar��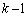 �d���ɂ����܂��B
�d���ɂ����܂��B
���̗��ӂ�x�Ŕ�������ƁA
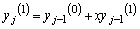 �@����B
�@����B�����x�Ŕ�������ƁA
�����x�Ŕ�������ƁA
������A
(�T) 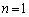 �̂Ƃ��A�B���A�\���͐��藧���܂��B
�̂Ƃ��A�B���A�\���͐��藧���܂��B (�U) 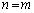 �̂Ƃ��A�\�������藧�Ɖ��肵�āA
�̂Ƃ��A�\�������藧�Ɖ��肵�āA ���ӂ�x�Ŕ�������ƁA
����āA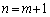 �̂Ƃ��ɂ��\���͐��藧���܂��B
�̂Ƃ��ɂ��\���͐��藧���܂��B (�T)�C(�U)���An�����R���̂Ƃ��A�\���͐��藧���܂��B
�� 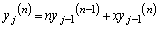 ......[��]
......[��]
(4) k�Ɋւ��鐔�w�I�A�[�@�ɂ��ؖ����܂��B
(�T)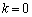 �̂Ƃ��A(1)���A����r��n��������(B)�̉��ł���Ƃ��A
�̂Ƃ��A(1)���A����r��n��������(B)�̉��ł���Ƃ��A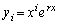 (
(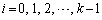 )��i�́A
)��i�́A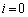 �Ɍ����A
�Ɍ����A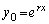 �͔���������(A)�����̂ŁA��ӂ͐��藧���܂��B
�͔���������(A)�����̂ŁA��ӂ͐��藧���܂��B (�U)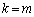 �̂Ƃ��A��ӂ����藧�Ɖ��肵�܂��B�����A����r��n��������(B)��m�d���ł���Ƃ��A
�̂Ƃ��A��ӂ����藧�Ɖ��肵�܂��B�����A����r��n��������(B)��m�d���ł���Ƃ��A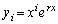 (
(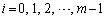 )�͔���������(A)�����Ɖ��肵�܂��B
)�͔���������(A)�����Ɖ��肵�܂��B �����ŁA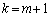 �̏ꍇ���l���܂��B�܂�A����r��n��������(B)��
�̏ꍇ���l���܂��B�܂�A����r��n��������(B)��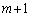 �d�����Ƃ��܂��B
�d�����Ƃ��܂��B
���̂Ƃ��A����r��n��������(B)��m�d���ɂȂ��Ă���̂ŁA(�U)�̉�����A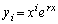 (
(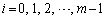 )�͔���������(A)�����܂��B�]���āA
)�͔���������(A)�����܂��B�]���āA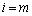 �̏ꍇ��
�̏ꍇ��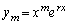 ������������(A)�������Ƃ�������A�u
������������(A)�������Ƃ�������A�u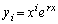 (
(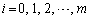 )������������(A)�����v���Ƃ������āA
)������������(A)�����v���Ƃ������āA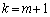 �̏ꍇ�ɂ���ӂ����藧���Ƃ��������Ƃ��ł��܂��B(3)�̌��ʂ�
�̏ꍇ�ɂ���ӂ����藧���Ƃ��������Ƃ��ł��܂��B(3)�̌��ʂ�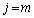 �Ƃ��āA
�Ƃ��āA ������
����ɁA
�������A
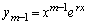 �͔���������(A)�����̂ŁA2�Ԗڂ̒��J�b�R���́A
�͔���������(A)�����̂ŁA2�Ԗڂ̒��J�b�R���́A�ł��B1�Ԗڂ̒��J�b�R�����l���܂��B����r��n��������(B)��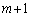 �d���ł���Ƃ��A(2)���A������
�d���ł���Ƃ��A(2)���A������ ��r��m�d���ɂ����܂��B����ƁA(�U)�̉���ɂ����āA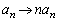 �C
�C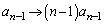 �C����C
�C����C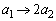 �C
�C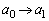 �ƌ��邱�Ƃɂ��A
�ƌ��邱�Ƃɂ��A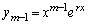 �́A����������
�́A���������� �����܂��B�܂�A1�Ԗڂ̒��J�b�R����
�ƂȂ�܂��B
�]���āA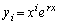 (
(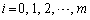 )������������(A)�����A
)������������(A)�����A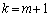 �̏ꍇ�ɂ���ӂ����藧���܂��B
�̏ꍇ�ɂ���ӂ����藧���܂��B (�T)�C(�U)���Ak�����R���Ƃ��āA����r��n��������(B)��k�d���ł���Ƃ��A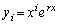 (
(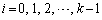 )�͔���������(A)�����܂��B
)�͔���������(A)�����܂��B
�NjL�D(A)�̂悤�Ȕ�������������`�����������ƌ����܂��B��R�͂�����ꍇ�̐U�����ۂ�A�d���C�w�ɂ�����RLC��H�̋����ׂ�ꍇ�Ȃǂɏo�Ă��܂��B �ȉ��A�ō����̌W����1���Ƃ��Đ��`�����������ɂ��čl���܂��B
(1) ���`1�K�����������F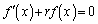 �@(r�F�萔)
�@(r�F�萔) ���ӂ�ϕ����āA
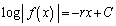 (C�F�ϕ��萔)
(C�F�ϕ��萔)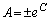 �Ƃ����āA
�Ƃ����āA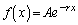 �@(A�F�萔)
�@(A�F�萔)���l�ɂ��āA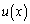 ��^����ꂽ�����Ƃ��āA
��^����ꂽ�����Ƃ��āA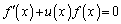 �̉��́A
�̉��́A 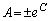 �Ƃ����āA
�Ƃ����āA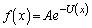 �@����C
�@����C�ȏ�̏ꍇ��Ď����`1������������ƌ����܂��B���̕��������Ď����`1������������ƌ����܂��B
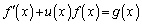 �@����D
�@����D���̏ꍇ�̉��́A�C��A����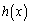 �ɒu�������A
�ɒu�������A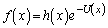 ������������D�ɑ�����A
������������D�ɑ�����A �D���A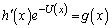 �C
�C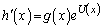
�� 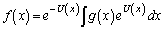
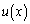 ����
����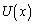 �����߁A�ϕ��v�Z���s�����Ƃɂ��
�����߁A�ϕ��v�Z���s�����Ƃɂ��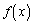 �����߂��܂��B
�����߂��܂��B (2) ���`2�K�����������F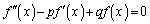 �@(p�Cq�F�萔)
�@(p�Cq�F�萔) 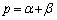 �C
�C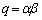 (
(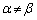 )�Ƃ��āA�����������F
)�Ƃ��āA�����������F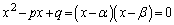
���̂Ƃ��A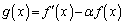 �Ƃ����ƁA
�Ƃ����ƁA�ƂȂ�̂ŁA(1)�̏ꍇ�̌��ʂ�p���āA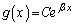 (C�F�萔)������A
(C�F�萔)������A ���̉���(1)�̔�Ď��̏ꍇ�̌��ʂ�p���āA
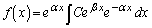 �@����E
�@����E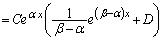 �@(D�F�萔)
�@(D�F�萔)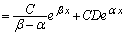
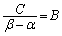 �C
�C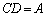 �ƒu�������āA
�ƒu�������āA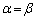 �̏ꍇ(�������������d��α�����ꍇ)�́A�E���A
�̏ꍇ(�������������d��α�����ꍇ)�́A�E���A�ƂȂ�܂��B
(3) ���`n�K����������
�{��̂悤�Ȑ��`�����������́A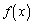 ��
��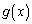 �����ł���A
�����ł���A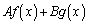 �����ɂȂ�܂��B�{����An���̓������������قȂ�n�̉�
�����ɂȂ�܂��B�{����An���̓������������قȂ�n�̉�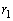 �C
�C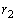 �C����C
�C����C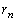 �����ĂA����������(A)�̈�ʉ��́A
�����ĂA����������(A)�̈�ʉ��́A n���̓������������قȂ�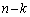 �̉�
�̉�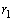 �C����C
�C����C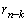 ��k�d��R�����ĂA����������(A)�̈�ʉ��́A
��k�d��R�����ĂA����������(A)�̈�ʉ��́A �ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B