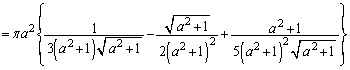九大理系数学'10年後期[1]
直線 (ただしaは正の実数)をlとし、曲線
(ただしaは正の実数)をlとし、曲線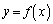 (ただし
(ただし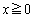 )をCとする。曲線Cが直線lの下側にあり、曲線C上の点
)をCとする。曲線Cが直線lの下側にあり、曲線C上の点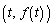 と直線lとの距離が
と直線lとの距離が で表されるとき、以下の問いに答えよ。
で表されるとき、以下の問いに答えよ。
1.関数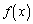 を求めよ。
を求めよ。 2.曲線Cとx軸で囲まれた図形を、x軸のまわりに回転させてできる回転体の体積Vを求めよ。
3.Vが最大となるようにaの値を定めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 標準的な微積分の計算問題ですが、3.では少し工夫します。
1.直線l: と、曲線C上の点
と、曲線C上の点 との距離が
との距離が であることから、
であることから、 曲線Cが直線lの下側にあることから、 ,よって、
,よって、 ∴ 
t をxに入れ替えて、 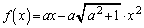 ......[答]
......[答]
2. とすると、
とすると、 ∴ 
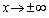 のとき、
のとき、
曲線Cとx軸で囲まれた図形は、 の範囲に存在します。
の範囲に存在します。
3. のままaで微分するのでは計算が大変になることは見えています。
のままaで微分するのでは計算が大変になることは見えています。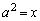 などとおくのでは分母の形が簡単にならずに不利です。分母を簡単にするのであれば、
などとおくのでは分母の形が簡単にならずに不利です。分母を簡単にするのであれば、 とおけばVが微分しやすい形になります。
とおけばVが微分しやすい形になります。 増減表より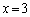 のときV最大(関数の増減を参照)となります。このとき、
のときV最大(関数の増減を参照)となります。このとき、 ,
,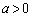 より、
より、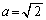 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。