���k�嗝�n���w'10�N�O��[2]
a�Cb�𐳂̎����Ƃ���B�Ȑ�C�F �Ɠ_P
�Ɠ_P ���l����B�ȉ��̖₢�ɓ�����B
���l����B�ȉ��̖₢�ɓ�����B
(1) �_P����Ȑ�C�ɐڐ������傤��3�{������悤�ȓ_ �̑��݂���̈��}������B
�̑��݂���̈��}������B (2) �_P����Ȑ�C�ɐڐ������傤��2�{������Ƃ���B2�̐ړ_��A�CB�Ƃ����Ƃ��A ��
�� ��菬�����Ȃ邽�߂�a��b�̏��������߂�B
��菬�����Ȃ邽�߂�a��b�̏��������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶���悭�ǂ�Ŋ��Ⴂ�̂Ȃ��悤�ɂ��悤�A�Ƃ������ł��B
 �@����@
�@����@
(1)  �@����A
�@����A �ړ_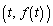 �ɂ������ڐ��́A
�ɂ������ڐ��́A �_P ����������ڐ��Ȃ̂ŁA
����������ڐ��Ȃ̂ŁA ��������ƁA
��������ƁA �ł��B
�ł��B ��  �@����B
�@����B
���̍��ӂ� �Ƃ����܂��B�B��
�Ƃ����܂��B�B�� �ł��B
�ł��B �ɑ�l�F
�ɏ��l�F
���Ƃ�܂�(3�����̑������Q��)�B
�_P����Ȑ�C�ɐڐ������傤��3�{������悤�ɂ��邽�߂ɂ́At��3�������� �����قȂ�3�����������Ă悢�̂ł����A���̂��߂ɂ́A�ɑ�l�����ł��ɏ��l�����ƂȂ邱�Ƃ��K�v�\���ł�(�����@�̕������ւ̉��p���Q��)�B
�����قȂ�3�����������Ă悢�̂ł����A���̂��߂ɂ́A�ɑ�l�����ł��ɏ��l�����ƂȂ邱�Ƃ��K�v�\���ł�(�����@�̕������ւ̉��p���Q��)�B �ɑ�l�F
���A
�ƂȂ�܂����A���̂Ƃ��K���A
�ɏ��l�F
�Ȃ̂ŁA �����قȂ�3���������������́A
�����قȂ�3���������������́A �ł��B
�ł��B �C
�C ���A�_
���A�_ �̑��݂���̈��}������ƉE�}���ΐF���F��(�_���̏c���A���E����A�y�є��}��������)�B
�̑��݂���̈��}������ƉE�}���ΐF���F��(�_���̏c���A���E����A�y�є��}��������)�B
(2) �_P����Ȑ�C�ɐڐ������傤��2�{������Ƃ��A�B�F �����قȂ��������2�����܂��B�܂�A�B�F
�����قȂ��������2�����܂��B�܂�A�B�F ���d����1�����܂��B���̂Ƃ��A
���d����1�����܂��B���̂Ƃ��A �̃O���t�͉����Ɛڂ���悤�ɂȂ�̂ŁA�ɑ�l���ɏ��l�̂����ꂩ��0�ɂȂ�܂��B
�̃O���t�͉����Ɛڂ���悤�ɂȂ�̂ŁA�ɑ�l���ɏ��l�̂����ꂩ��0�ɂȂ�܂��B  �̂Ƃ��͋ɑ�l�����ƂȂ�B�̎�������1�ł��B
�̂Ƃ��͋ɑ�l�����ƂȂ�B�̎�������1�ł��B �ł�
�ł� �ł�
�ł� �Ȃ̂ŁA�ɏ��l��0�ɂȂ邱�Ƃ͂Ȃ��A�ɑ�l��0���Ƃ���ƁA
�Ȃ̂ŁA�ɏ��l��0�ɂȂ邱�Ƃ͂Ȃ��A�ɑ�l��0���Ƃ���ƁA ���A
���A �@����C
�@����C���̂Ƃ��A
�́A2���A �C
�C �������܂��B�܂�A2�ړ_��x���W�́A0��
�������܂��B�܂�A2�ړ_��x���W�́A0�� �ł��B2�ڐ��̌X���́A�A���A
�ł��B2�ڐ��̌X���́A�A���A ��
�� �ł��B
�ł��B
���ڐ���x���Ƃ̂Ȃ��p��α�Cβ�Ƃ��āA �C
�C ���A���ڐ��̂Ȃ��p
���A���ڐ��̂Ȃ��p �́A
�́A  ��
�� ��菬�����Ȃ邽�߂ɂ́A2�ڐ��̂Ȃ��p��
��菬�����Ȃ邽�߂ɂ́A2�ڐ��̂Ȃ��p�� �ƂȂ�悢�̂ł����A���̂Ƃ��A
�ƂȂ�悢�̂ł����A���̂Ƃ��A �ƂȂ�̂ŁA
�ƂȂ�̂ŁA �@����D
�@����D�C�C�D���A���߂�����́A
 ����
����  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B