東北大文系数学'10年後期[2]
△OABにおいて、辺OAを1:1に内分する点をM,辺OBを2:1に内分する点をNとし、線分ANと線分BMの交点をPとする。以下の問いに答えよ。
(2) 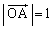 とする。辺OAを含む直線をl,辺OBを含む直線をmとする。△ABPの外接円がl,mに接するとき、内積
とする。辺OAを含む直線をl,辺OBを含む直線をmとする。△ABPの外接円がl,mに接するとき、内積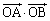 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1)は2通りの解法を書いておきます。教科書通りの解法と、別解のおすすめ解法です。(2)はかなり面倒で、無闇に計算すると何をやっているのかわからなくなります。

(1) M,P,Bが一直線上の点であることから、MP:PB =  :t として、
:t として、 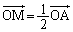 より、
より、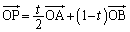 ・・・①
・・・①N,P,Aが一直線上の点であることから、NP:PA =  :s として、
:s として、 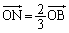 より、
より、 ・・・②
・・・② ,
, が1次独立であることから、①,②の係数を比較して、
が1次独立であることから、①,②の係数を比較して、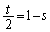 ,
,
連立して解くと、
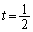 ,
,
①より、
 ......[答]
......[答]∴ MP:PB = 1:1
よって、
(2) △ABPの外接円の中心をQとします。
外接円がl,mに接するので、 ,
,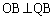 ,これより、
,これより、 ∴ 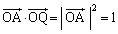 ・・・③
・・・③ ∴  また、△OAQ≡△OBQより、
また、△OAQ≡△OBQより、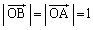 ,
,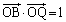 ・・・④
・・・④
一方、点Qは、辺PAの垂直二等分線と辺PBの垂直二等分線の交点です。PA,PBの中点をC,Dとすると、 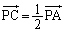 ,
, ・・・⑤
・・・⑤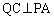 より、
より、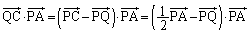 (∵ ⑤)
(∵ ⑤)ところで、(1)の結果より、
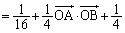 (∵ ③,④)
(∵ ③,④)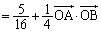 ・・・⑦
・・・⑦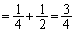 (∵ ③,④) ・・・⑧
(∵ ③,④) ・・・⑧⑦,⑧を⑥に代入して、
∴ 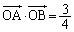 ......[答]注.(2)の計算のポイントは、③,④をうまく利用できるかというところにあります。
......[答]注.(2)の計算のポイントは、③,④をうまく利用できるかというところにあります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。