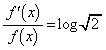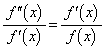���u�Б嗝�H���w'11�N[4]
����
�͑Q����
 �@(
�@(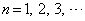 )
)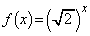 �Ƃ��Ď��̖�ɓ�����B
�Ƃ��Ď��̖�ɓ�����B
(1) 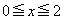 �ɂ�����
�ɂ�����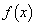 �̍ő�l�ƍŏ��l�����߂�B
�̍ő�l�ƍŏ��l�����߂�B (2) 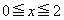 �ɂ�����
�ɂ�����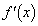 �̍ő�l�ƍŏ��l�����߂�B
�̍ő�l�ƍŏ��l�����߂�B (3)  (
(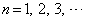 )���������邱�Ƃ𐔊w�I�A�[�@��p���Ď����B
)���������邱�Ƃ𐔊w�I�A�[�@��p���Ď����B (4) 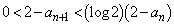 (
(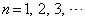 )���������邱�Ƃ������B
)���������邱�Ƃ������B (5) 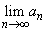 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����Ȃ�A �H�ƕ������ƌ������ł����A���J�ȗU�������Ă���̂ŁA�U���ʂ�ɐi�߂čs���Ήł��܂��B
�H�ƕ������ƌ������ł����A���J�ȗU�������Ă���̂ŁA�U���ʂ�ɐi�߂čs���Ήł��܂��B
(1) 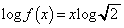
�ő�l�F2�C�ŏ��l�F1 ......[��]
(2) 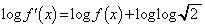
�ΐ������@�ɂ���Ĕ�������ƁA
����āA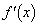 �͒P���������ł��B
�͒P���������ł��B
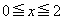 �ɂ����āA
�ɂ����āA
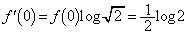 �C
�C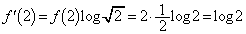 ���A
���A �ő�l�F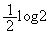 �C�ŏ��l�F
�C�ŏ��l�F ......[��]
......[��]
(�T) 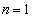 �̂Ƃ��A
�̂Ƃ��A ���A�������܂��B
���A�������܂��B (�U) 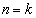 �̂Ƃ��A
�̂Ƃ��A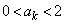 ����������Ɖ��肵�܂��B
����������Ɖ��肵�܂��B (1)���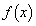 �͒P���������Ȃ̂ŁA
�͒P���������Ȃ̂ŁA
����āA �ƂȂ�A
�ƂȂ�A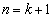 �̂Ƃ����������܂��B
�̂Ƃ����������܂��B (�T)�C(�U)���A (
( )���������܂��B
)���������܂��B
(4) 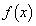 �͑S�����ɂ����ĘA���������\�Ȋ��Ȃ̂ŁA���ϒl�̒藝���g���܂��B���ϒl�̒藝���A
�͑S�����ɂ����ĘA���������\�Ȋ��Ȃ̂ŁA���ϒl�̒藝���g���܂��B���ϒl�̒藝���A ��������c�����݂��܂��B(2)���A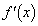 �͒P���������Ȃ̂ŁA
�͒P���������Ȃ̂ŁA �C����āA
�C����āA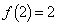 �C
�C ���A
���A �� 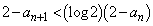 �@(
�@( )
)
(5) (4)�̌��ʂ��A
 �C
�C ���A
���A�����ŁA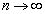 �Ƃ���ƁA
�Ƃ���ƁA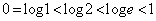 ���A
���A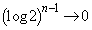 �@(���䐔��̋Ɍ����Q��)�͂��݂����̌������A
�@(���䐔��̋Ɍ����Q��)�͂��݂����̌������A
��  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B