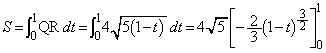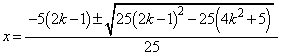�d�ʑ吔�w'11�N�O��[4]
����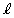 �F
�F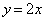 �̖@���x�N�g����
�̖@���x�N�g����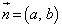 �Ƃ��A�_P
�Ƃ��A�_P �ƒ���
�ƒ��� �Ƃ̋�����h�Ƃ���B�������A
�Ƃ̋�����h�Ƃ���B�������A �ŁA
�ŁA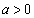 �Ƃ���B
�Ƃ���B
�ȉ��̖₢�ɓ�����B
(1) 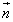 �̐���a�Cb�����߂�B
�̐���a�Cb�����߂�B (2) ���_��O�Ƃ��A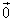 �łȂ�
�łȂ�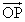 �ɑ��A
�ɑ��A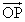 ��
��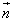 �̂Ȃ��p��θ �Ƃ���B
�̂Ȃ��p��θ �Ƃ���B ���̂Ƃ��Ah��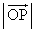 ��θ ��p���ĕ\���B�܂��Ah��x�Cy��p���ĕ\���B
��θ ��p���ĕ\���B�܂��Ah��x�Cy��p���ĕ\���B �ȉ��ł́A�Ȑ�C���A�_A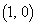 �ƒ���
�ƒ��� ����̋������������_P
����̋������������_P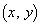 �̋O�ՂƂ���B
�̋O�ՂƂ���B
(3) �Ȑ�C�̕�����(x�Cy�̊W��)�����߂�B
(4) �Ȑ�C�ƒ��� (t �͒萔)�Ƃ̋��L�_�̌������߂�B
(t �͒萔)�Ƃ̋��L�_�̌������߂�B (5) �Ȑ�C�ƒ���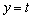 ��2�̋��L�_Q�CR�����Ƃ��A����QR�̒�����t ��p���ĕ\���B
��2�̋��L�_Q�CR�����Ƃ��A����QR�̒�����t ��p���ĕ\���B (6) �Ȑ�C�ƒ���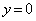 �Ƃň͂܂�镔���̖ʐ�S�����߂�B
�Ƃň͂܂�镔���̖ʐ�S�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ȑ�C�́A���ɑ��ČX���Ă��܂����A�������̒�`�����Ă��܂��B(6)�̖ʐς͉�]�ɂ�炸�Ƃ�(5)�����p���ē����邱�Ƃ��ł��܂��B
(1) ����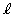 ��̓_�Ō��_�ȊO�̓_�A�Ⴆ�Γ_B
��̓_�Ō��_�ȊO�̓_�A�Ⴆ�Γ_B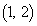 ���l���܂��B����
���l���܂��B����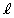 �̕����x�N�g��
�̕����x�N�g�� �Ɛ����ȃx�N�g����
�Ɛ����ȃx�N�g����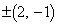 (�������Q��)�C����āA
(�������Q��)�C����āA ���A
���A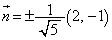 �C
�C �Ƃ���
�Ƃ���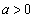 ���A
���A �C
�C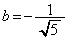 ......[��]
......[��]
(2) �_P���璼�� �ɉ��낵�������̑���H�Ƃ��܂��B
�ɉ��낵�������̑���H�Ƃ��܂��B 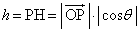 ......[��]
......[��]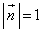 ���A
���A�܂��A
����āA
 ......[��]
......[��]
(3) 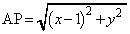 ���A
���A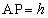 �̂Ƃ��A
�̂Ƃ��A ���ӂ�2�悷��ƁA
��  ......[��]�@����@
......[��]�@����@
(4)  �̂Ƃ��A
�̂Ƃ��A 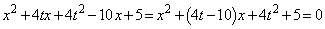 �@����A
�@����A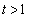 �̂Ƃ�
�̂Ƃ�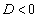 �ƂȂ�A���L�_��0�A
�ƂȂ�A���L�_��0�A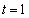 �̂Ƃ�
�̂Ƃ�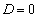 �ƂȂ�A���L�_��1�A
�ƂȂ�A���L�_��1�A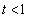 �̂Ƃ�
�̂Ƃ�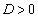 �ƂȂ�A���L�_��2�� ......[��]
�ƂȂ�A���L�_��2�� ......[��]
(5) �Ȑ�C�ƒ���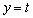 ��2�̋��L�_Q�CR�����Ƃ��A�܂�A
��2�̋��L�_Q�CR�����Ƃ��A�܂�A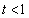 �̂Ƃ��A�������A�������ƁAQ�CR��x���W�́A
�̂Ƃ��A�������A�������ƁAQ�CR��x���W�́A ����QR�̒����́AQ�CR��x���W�̍��Ƃ��āA
 ......[��]
......[��]
(6) (4)������QR�����݂���̂́AQ��R����v����ꍇ���܂߂āA �̂Ƃ��ł��B�]���āA���߂�ʐ�S��(��ϕ��Ɩʐ����Q��)�A
�̂Ƃ��ł��B�]���āA���߂�ʐ�S��(��ϕ��Ɩʐ����Q��)�A 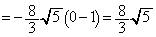 ......[��]
......[��]
�NjL�D�������@�ŕ\�����Ȑ�C�́A����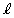 �������A�_A
�������A�_A ���œ_�Ƃ���������ł��B������C��x���Ay���ɑ��ČX���Ă��܂����A�������̎��́A����
���œ_�Ƃ���������ł��B������C��x���Ay���ɑ��ČX���Ă��܂����A�������̎��́A����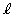 �ɐ�����A��ʂ钼���F
�ɐ�����A��ʂ钼���F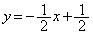 �ł��B
�ł��B ���� �ɕ��s�Ȓ����F
�ɕ��s�Ȓ����F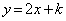 �ƕ�����C�Ƃ̌�_�����߂�ƁA�@��
�ƕ�����C�Ƃ̌�_�����߂�ƁA�@��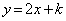 ��A�����A
��A�����A �������āA
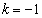 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�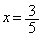 (�d��)�C
(�d��)�C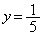 �ƂȂ�܂����A
�ƂȂ�܂����A �͕�����C�̒��_�ł��B
�͕�����C�̒��_�ł��B
 �̂Ƃ���2��_�ƂȂ�܂����A2��_�͎��F
�̂Ƃ���2��_�ƂȂ�܂����A2��_�͎��F ��̓_
��̓_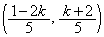 �Ɋւ��đΏ̂Ȉʒu�ɂ���܂��B
�Ɋւ��đΏ̂Ȉʒu�ɂ���܂��B
������C�̒��_�Əœ_�̋�����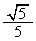 �ł��B
�ł��B
������C���A�������̎���y���A���_�����_�A�œ_�� �ɗ���悤�ɉ�]������ƁA������C�́A
�ɗ���悤�ɉ�]������ƁA������C�́A ���A
���A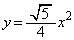 �ƂȂ�܂��B
�ƂȂ�܂��B
����x�����悤�ɉ�]������ƁA�_ ��ʂ�X��
��ʂ�X�� �̒����F
�̒����F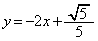 �ƂȂ�܂��B
�ƂȂ�܂��B
 ��
��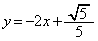 ��A������ƁA
��A������ƁA
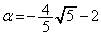 �C
�C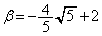 �Ƃ��āA(6)�̖ʐ�S�́A
�Ƃ��āA(6)�̖ʐ�S�́A�Ȃ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B