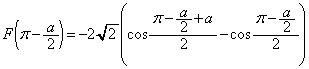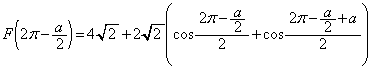北大理系数学'11年前期[5]
 とする。
とする。 に対して
に対して
と定める。
(1) 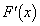 を求めよ。
を求めよ。 (2) 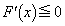 となるxの範囲を求めよ。
となるxの範囲を求めよ。 (3)  の極大値および極小値を求めよ。
の極大値および極小値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 難問というわけではありませんが、積分範囲 が被積分関数
が被積分関数 の微分不可能な点
の微分不可能な点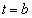 を含むとき、公式を使って、
を含むとき、公式を使って、
としても良いのか、という問題があります。根号を含むような関数、例えば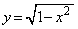 のような関数は、根号内が0になるところ
のような関数は、根号内が0になるところ において微分不可能(微分・導関数を参照)なので、根号がつく関数では注意が必要です。
において微分不可能(微分・導関数を参照)なので、根号がつく関数では注意が必要です。
を考えてみます。
微分可能な関数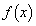 が
が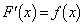 を満たし、
を満たし、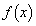 が
が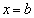 の前後で符号をプラスからマイナスに変えるとします。つまり、
の前後で符号をプラスからマイナスに変えるとします。つまり、 において
において ,
, ,
,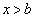 において
において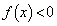 だとします。
だとします。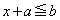 となるとき、
となるとき、
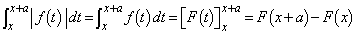
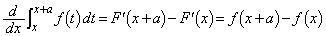 ・・・①
・・・①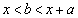 となるとき、
となるとき、
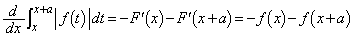 ・・・②
・・・②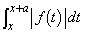 は、
は、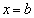 において連続なのですが、①と②では、
において連続なのですが、①と②では、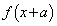 の符号が異なることに注意が必要です。一般的には、積分範囲内に被積分関数の微分不可能な点がある場合、(*)は使えません。
の符号が異なることに注意が必要です。一般的には、積分範囲内に被積分関数の微分不可能な点がある場合、(*)は使えません。
(1) 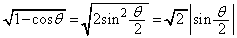
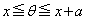 の範囲で
の範囲で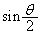 の符号がどうなるかが問題ですが、
の符号がどうなるかが問題ですが、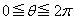 であれば
であれば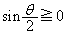 ,
,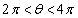 であれば
であれば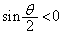 です。従って、
です。従って、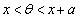 の範囲が
の範囲が を含むとき、つまり、
を含むとき、つまり、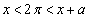 のとき、
のとき、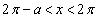 となりますが、このときは、積分区間を分けて考える必要があります(絶対値を含む定積分を参照)。
となりますが、このときは、積分区間を分けて考える必要があります(絶対値を含む定積分を参照)。(i)  のとき、
のとき、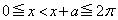 となるので、
となるので、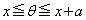 の範囲において、
の範囲において、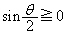 となり、
となり、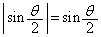 です。よって、
です。よって、 (ii)  のとき、上記より、
のとき、上記より、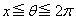 においては
においては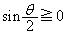 で、
で、 ですが、
ですが、 においては
においては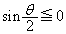 で、
で、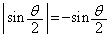 です。積分区間を分けて、
です。積分区間を分けて、 ところで、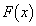 は、
は、 (i)において、
(ii)において、 のとき、
のとき、 なので、連続です。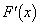 は、
は、 (i)において、
(ii)において、
なので、やはり連続です。つまり、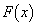 は
は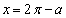 においても微分可能です。以上より、
においても微分可能です。以上より、 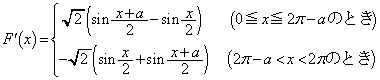 ......[答]
......[答]追記.公式: を使えば、
を使えば、 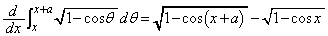 ・・・③
・・・③となります。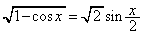 ですが、
ですが、
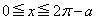 のとき
のとき
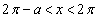 のとき
のとき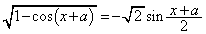 (
(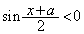 )となるので、③を解答としてOKです。但し、上記の問題点は隠れてしまいます。
)となるので、③を解答としてOKです。但し、上記の問題点は隠れてしまいます。
(2) (i)  のとき、
のとき、 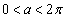 のとき、
のとき、 と(1)の結果より、
と(1)の結果より、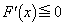 となるのは、
となるのは、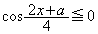 のときで、
のときで、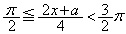 のとき、つまり、
のとき、つまり、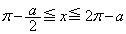 (
(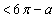 )のときです。
)のときです。(ii)  のとき、
のとき、 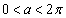 のとき、
のとき、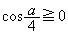 と(1)の結果より、
と(1)の結果より、 となるのは、
となるのは、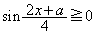 のときで、
のときで、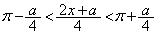 なので
なので のとき、つまり、
のとき、つまり、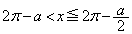 のときです。
のときです。(i),(ii)で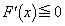 となる範囲は、境界
となる範囲は、境界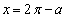 のところでつながっていて、
のところでつながっていて、 ......[答]
......[答]
(3) 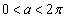 より、
より、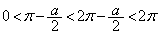 となるので、次の増減表が得られます。
となるので、次の増減表が得られます。 極大値: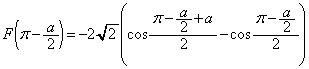
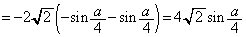 ......[答]
......[答]極小値: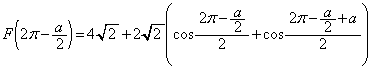
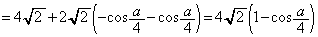 ......[答]
......[答]注意.極大は(1)(2)の(i)の範囲に、極小は(1)(2)の(ii)の範囲にあります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 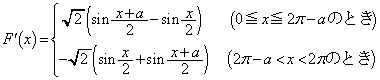 ......[答]
......[答]