��嗝�n���w'11�N���[2]
 �܂���
�܂���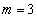 �Ƃ���Bn�����R���Ƃ��A1�ȏ�n�ȉ��̐����l���Ƃ�m���̐���
�Ƃ���Bn�����R���Ƃ��A1�ȏ�n�ȉ��̐����l���Ƃ�m���̐���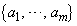 �̂����A
�̂����A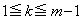 �ɑ���
�ɑ��� �������̂̌���
�������̂̌��� �Ƃ���B
�Ƃ���B
(1) 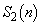 �����߂�B
�����߂�B (2) 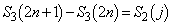 �������R��j�����߂�B
�������R��j�����߂�B (3) �Ɍ��l �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@'85�N[1]���v�킹��悤�Ȗ��ł����A���ǂ́A��Ԃ̊i�q�_�̐������߂���ł��B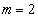 �͕��ʏ�̊i�q�_�A
�͕��ʏ�̊i�q�_�A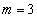 �͋�ԓ��̊i�q�_�A�Ƃ������Ƃł��B(3)�́A�����Ɍv�Z���Ȃ��Ă��A�͂��݂����ɂ��邱�Ƃ�z�肵�ĕs�����̌`�����悤�ɂ��܂��傤�B
�͋�ԓ��̊i�q�_�A�Ƃ������Ƃł��B(3)�́A�����Ɍv�Z���Ȃ��Ă��A�͂��݂����ɂ��邱�Ƃ�z�肵�ĕs�����̌`�����悤�ɂ��܂��傤�B
�܂��́A(1)�̈Ӗ������߂Ȃ��Ɛ�ɐi�߂Ȃ��̂ŁA �Ƃ��āA��̓I�ȏꍇ�ׂĂ݂܂��B
�Ƃ��āA��̓I�ȏꍇ�ׂĂ݂܂��B
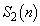 ���l����̂ŁA
���l����̂ŁA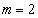 �Ƃ��܂��B
�Ƃ��܂��B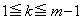 ����k�́A
����k�́A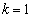 �݂̂ŁA
�݂̂ŁA �ƂȂ�܂��B
�ƂȂ�܂��B
 �̂Ƃ��A
�̂Ƃ��A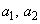 �Ƃ���1�����Ƃ蓾�Ȃ��̂ł����A����ł́A
�Ƃ���1�����Ƃ蓾�Ȃ��̂ł����A����ł́A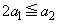 �͖�������܂���B
�͖�������܂���B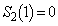 �ł��B
�ł��B
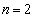 �̂Ƃ��A
�̂Ƃ��A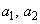 �́A1��2���Ƃ蓾��̂ł����A
�́A1��2���Ƃ蓾��̂ł����A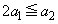 �����̂́A
�����̂́A �C
�C �̏ꍇ�݂̂ŁA
�̏ꍇ�݂̂ŁA �ł��B
�ł��B
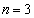 �̂Ƃ��A
�̂Ƃ��A �́A1��2��3���Ƃ蓾��̂ł����A
�́A1��2��3���Ƃ蓾��̂ł����A ��������́A
��������́A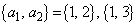 �݂̂ŁA
�݂̂ŁA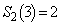 �ł��B
�ł��B
 �̂Ƃ��A
�̂Ƃ��A �́A1��2��3��4���Ƃ蓾��̂ł����A
�́A1��2��3��4���Ƃ蓾��̂ł����A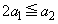 ��������́A
��������́A �݂̂ŁA
�݂̂ŁA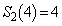 �ł��B
�ł��B
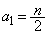 �C
�C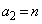 �Ƃ����g�ݍ��킹�́An�������̂Ƃ��ɂ͉\�ł����An����̂Ƃ��ɂ͉\�łȂ��̂ŁAn������������ŏꍇ�������čl���邱�ƂɂȂ�܂��B
�Ƃ����g�ݍ��킹�́An�������̂Ƃ��ɂ͉\�ł����An����̂Ƃ��ɂ͉\�łȂ��̂ŁAn������������ŏꍇ�������čl���邱�ƂɂȂ�܂��B
(1) j�����R���Ƃ��܂��B
�E �̂Ƃ��A
�̂Ƃ��A 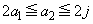 �@����@
�@����@�������R��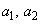 �̑g�̌��𐔂��邱�ƂɂȂ�܂��B
�̑g�̌��𐔂��邱�ƂɂȂ�܂��B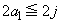 �Ȃ̂�
�Ȃ̂�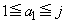 �ł��B���͈̔͂�
�ł��B���͈̔͂�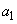 �̒l��1���߂�ƁA�@�������R��
�̒l��1���߂�ƁA�@�������R��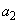 �́A
�́A �ʂ�̒l���Ƃ蓾�܂��B����āA
�ʂ�̒l���Ƃ蓾�܂��B����āA �E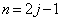 �̂Ƃ��A
�̂Ƃ��A 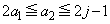 �@����A
�@����A�������R��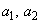 �̑g�̌��𐔂��邱�ƂɂȂ�܂��B
�̑g�̌��𐔂��邱�ƂɂȂ�܂��B �Ȃ̂ŁA
�Ȃ̂ŁA �C
�C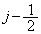 �͐����ł͂Ȃ��̂ŁA
�͐����ł͂Ȃ��̂ŁA �ƂȂ�܂��B���͈̔͂�
�ƂȂ�܂��B���͈̔͂� �̒l��1���߂�ƁA�A�������R��
�̒l��1���߂�ƁA�A�������R��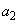 �́A
�́A �ʂ�̒l���Ƃ蓾�܂��B����āA
�ʂ�̒l���Ƃ蓾�܂��B����āA 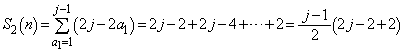 �@(���������
�@(���������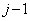 ���̘a)
���̘a)�ȏ���A
 ......[��]
......[��]
(2)  �C
�C �ł́A
�ł́A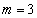 �Ȃ̂�3���̐���
�Ȃ̂�3���̐���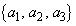 ���l���邱�ƂɂȂ�܂��B��ӂ��A
���l���邱�ƂɂȂ�܂��B��ӂ��A 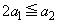 �C
�C
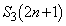 �ł́A
�ł́A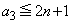
�]���� �́A
�́A �������R��
�������R��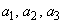 ����Ȃ鐔��
����Ȃ鐔�� �̌��ł��B
�̌��ł��B
 �ł́A
�ł́A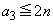
�]���� �́A
�́A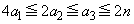 �������R��
�������R�� ����Ȃ鐔��
����Ȃ鐔��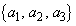 �̌��ł��B
�̌��ł��B
������A �́A
�́A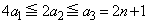 �C�܂�A
�C�܂�A (
(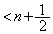 �C
�C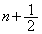 �͐����łȂ�)�ƂȂ鎩�R��
�͐����łȂ�)�ƂȂ鎩�R��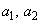 �̑g�̌��Ɉ�v���܂��B
�̑g�̌��Ɉ�v���܂��B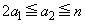 �ƂȂ鎩�R��
�ƂȂ鎩�R��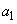 �C
�C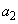 �̑g�̌��́A(1)���
�̑g�̌��́A(1)���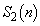 �ƂȂ�܂��B����āA
�ƂȂ�܂��B����āA �@����B
�@����B �������R��j�́A
�������R��j�́A ......[��]�܂��A
......[��]�܂��A �ł́A
�ł́A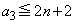
�]����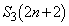 �́A
�́A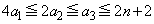 �������R��
�������R��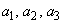 ����Ȃ鐔��
����Ȃ鐔�� �̌��ł��B
�̌��ł��B
 �Ɠ��l�ɁA
�Ɠ��l�ɁA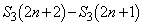 �́A
�́A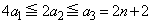 �C�܂�A
�C�܂�A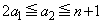 �ƂȂ鎩�R��
�ƂȂ鎩�R��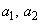 �̑g�̌�
�̑g�̌�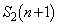 �Ɉ�v���܂��B����āA
�Ɉ�v���܂��B����āA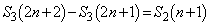 �@����C
�@����C
(3) �B�C�C���Aj�����R���Ƃ��āA
������
�ӁX������ƁA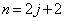 �̂Ƃ��A
�̂Ƃ��A ���l�ɁA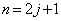 �̂Ƃ��A
�̂Ƃ��A 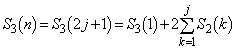 �@����E
�@����E �������R��
�������R�� �̑g�͑��݂��Ȃ��̂�
�̑g�͑��݂��Ȃ��̂�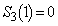
�D�C�E���A �C
�C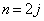 �ɂ�����炸�A
�ɂ�����炸�A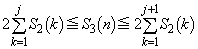 �@����F
�@����F�܂��A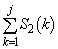 ��k�̋��ŏꍇ�������čl����͖̂ʓ|�Ȃ̂ŁA�͂��݂����ɂ��邱�Ƃ��l���āA(1)�̌��ʂ𗘗p���A
��k�̋��ŏꍇ�������čl����͖̂ʓ|�Ȃ̂ŁA�͂��݂����ɂ��邱�Ƃ��l���āA(1)�̌��ʂ𗘗p���A ����āA�F�́A
 �@����G
�@����G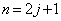 �̂Ƃ�
�̂Ƃ�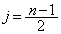 �C
�C �̂Ƃ�
�̂Ƃ� �ł����A
�ł����A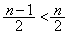 �Ȃ̂ŁA�G�̍��ӂ�
�Ȃ̂ŁA�G�̍��ӂ� �����������̂Ɣ�r���A�G�̉E�ӂ�
�����������̂Ɣ�r���A�G�̉E�ӂ� �����������̂Ɣ�r���܂��B
�����������̂Ɣ�r���܂��B
�G�̍��ӂɂ��āA�G�̉E�ӂɂ��āA
��  �e�ӂ�
�e�ӂ�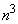 �Ŋ���A
�Ŋ���A 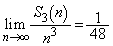 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 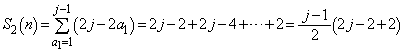 �@(���������
�@(��������� ......[��]
......[��]