�ꋴ�吔�w'06�N�O��[5]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�P�C2�C3�C4��1���L���ꂽ4���̃J�[�h������B�����̃J�[�h����1�����o�����ɖ߂��Ƃ������s��n��J��Ԃ��B�����o����n�̐��̘a��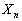 �Ƃ��A�ς�
�Ƃ��A�ς�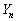 �Ƃ���B
�Ƃ���B
(1) 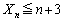 �ƂȂ�m����n�ŕ\���B
�ƂȂ�m����n�ŕ\���B (2) 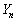 ��8�Ŋ�����m����n�ŕ\���B
��8�Ŋ�����m����n�ŕ\���B
���@(1)�͈�ʐ����������čl���悤�Ƃ���Ɠ��ł��B
(1) n�s���s���A�����o����n�̐��̘a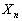 ���A
���A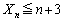 �ƂȂ�ꍇ�̐���
�ƂȂ�ꍇ�̐���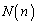 �Ƃ��āA�܂��A
�Ƃ��āA�܂��A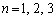 �ɂ��Ăǂ��Ȃ邩�ׂĂ݂܂��B
�ɂ��Ăǂ��Ȃ邩�ׂĂ݂܂��B (i) 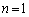 �̂Ƃ��A
�̂Ƃ��A 4���̃J�[�h�̂ǂ���o���Ă�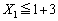 �����̂ŁA
�����̂ŁA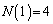 �ʂ�ł��B
�ʂ�ł��B (ii) 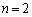 �̂Ƃ��A
�̂Ƃ��A 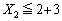 �@����@�@�ƂȂ�̂́A�ȉ��̏ꍇ�ł��B
�@����@�@�ƂȂ�̂́A�ȉ��̏ꍇ�ł��B�E1��ڂ�1���o���Ƃ��A
2��ڂ́A4���̃J�[�h�̂ǂ���o���Ă��@�����A4�ʂ�B
�E1��ڂ�2���o���Ƃ��A
2��ڂ́A1�C2�C3���o���Ƃ��ɇ@�����A3�ʂ�B
�E1��ڂ�3���o���Ƃ��A
2��ڂ́A1�C2���o���Ƃ��ɇ@�����A2�ʂ�B
�E1��ڂ�4���o���Ƃ��A
2��ڂ́A1���o���Ƃ��ɇ@�����A1�ʂ�B
����āA�@�����̂́A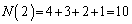 �ʂ�ł��B
�ʂ�ł��B (iii) 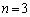 �̂Ƃ��A
�̂Ƃ��A 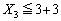 �@����A�@�ƂȂ�̂́A�ȉ��̏ꍇ�ł��B
�@����A�@�ƂȂ�̂́A�ȉ��̏ꍇ�ł��B�E1��ڂ�1���o���Ƃ��A
2��ځA3��ڂ�2��̐��̘a��5�ȉ��ɂȂ�Ƃ��ɇA�����A(ii)���A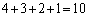 �ʂ�B
�ʂ�B �E1��ڂ�2���o���Ƃ��A
2��ځA3��ڂ�2��̐��̘a��4�ȉ��ɂȂ�Ƃ��ɇA�����A(ii)�Ɠ��l��(�a��5�ɂȂ�ꍇ�������Đ�����)�l����ƁA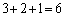 �ʂ�B
�ʂ�B �E1��ڂ�3���o���Ƃ��A
2��ځA3��ڂ�2��̐��̘a��3�ȉ��ɂȂ�Ƃ��ɇA�����A(ii)�Ɠ��l��(�a��5�C�a��4�ɂȂ�ꍇ�������Đ�����)�l����ƁA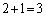 �ʂ�B
�ʂ�B �E1��ڂ�4���o���Ƃ��A
2��ځA3��ڂ�2��̐��̘a��2�ȉ��ɂȂ�Ƃ��ɇA�����܂����A����́A2��ڂ�3��ڂ�1���o���Ƃ��ŁA1�ʂ�B
����āA�A�����̂́A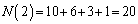 �ʂ�ł��B
�ʂ�ł��B �����܂ŗ���ƋK�����������Ă��܂��B
�����ƁA
�ɂȂ邾�낤�A�ƁA�\�������܂��B���̂܂ܑ����Ă����ƁA
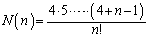 �@����B
�@����B�Ƃ������ƂɂȂ肻���ł����A��������w�I�A�[�@�Ŏ����̂ł́A���Ă������ɂ����ċ�J���邱�ƂɂȂ�܂��B
�����ŁA���j�]�������āA�B���Ⴄ�����Œ��߂邱�Ƃɂ��܂��B �Ȃ̂ŁA�B�������ό`����ƁA
�ƂȂ�A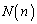 �́A�قȂ�
�́A�قȂ�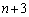 �̂��̂���n��I�ԑg�ݍ��킹�̐��ɂȂ肻���ł��B
�̂��̂���n��I�ԑg�ݍ��킹�̐��ɂȂ肻���ł��B
�����ŁA(i)�C(ii)�C(iii)������������悤�ȏꍇ�̐��̐��������l���邱�Ƃɂ��܂��B�Ⴆ�A(ii)��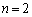 �̏ꍇ�ł́A
�̏ꍇ�ł́A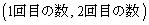 �Ƃ��āA
�Ƃ��āA �Ƃ���10�ʂ�Ɛ����Ă��܂����A������A�قȂ�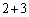 ����2��I�ԑg�ݍ��킹�̐��Ƃ��āA1����5�̐�������2������I�ԑI�ѕ��𐔂���ƁA
����2��I�ԑg�ݍ��킹�̐��Ƃ��āA1����5�̐�������2������I�ԑI�ѕ��𐔂���ƁA �̂悤�ɂȂ�܂��B2�̐�����������ׂ�ƁA��҂ł́A2��ڂ̐������A1��ڂ�2��ڂ̐����̘a�ɓ���ւ��Ă��邱�ƂɋC�Â��܂��B1��ڂɔ����o������1�`4�ɁA2��ڈȍ~1�`4�������Ă����̂ŁAi���(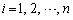 )�ɔ����o��������
)�ɔ����o��������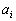 �Ƃ��āA
�Ƃ��āA �őg�ݍ��킹�̐��𐔂��Ă��A
�őg�ݍ��킹�̐��𐔂��Ă��A1��1�̑Ή�������̂ŁA�ꍇ�̐��ɕς��͂���܂���B�������A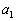 �C
�C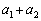 �C����C
�C����C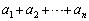 �́A
�́A �Ȃ̂ŁA�݂��ɑ��قȂ�n�̐����ł��B
�Ȃ̂ŁA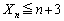 �ł���A
�ł���A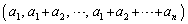 �́A1����
�́A1����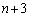 �܂ł̈قȂ�
�܂ł̈قȂ�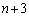 �̐�������n�̐�����I�Ԃ��ƂɂȂ�A���̑g�ݍ��킹�̐��́A
�̐�������n�̐�����I�Ԃ��ƂɂȂ�A���̑g�ݍ��킹�̐��́A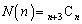 �ʂ�ł��B
�ʂ�ł��B
�������ŏ������ĂƂ��ẮA�ȉ��̂悤�ɂ܂Ƃ߂邱�Ƃ��ł���ł��傤�Bn��̎��s�̒��̑�i���(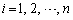 )�ɔ����o��������
)�ɔ����o��������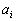 (
(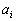 ��1�C2�C3�C4�̂����ꂩ)�Ƃ��A
��1�C2�C3�C4�̂����ꂩ)�Ƃ��A ��
��1��1�ɑΉ�������ƁA
���A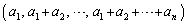 �́A
�́A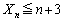 �̂Ƃ��A�قȂ�
�̂Ƃ��A�قȂ�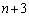 �̐�������n�̐�����I���̂ł���B���̑I�ѕ��A���Ȃ킿
�̐�������n�̐�����I���̂ł���B���̑I�ѕ��A���Ȃ킿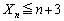 �ƂȂ�
�ƂȂ�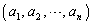 �̑I�ѕ��́A
�̑I�ѕ��́A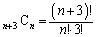 �ʂ肠��B
�ʂ肠��B
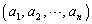 �̑I�ѕ���
�̑I�ѕ���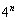 �ʂ肠���āA���̂ǂ�1�ʂ�����l�Ɋm���炵���B
�ʂ肠���āA���̂ǂ�1�ʂ�����l�Ɋm���炵���B
����āA���߂��m���́A 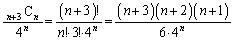 ......[��]
......[��]
(2) ��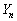 ��8�Ŋ�����ꍇ���l����Əꍇ��������ςȂ̂ŁA�]�����F�u
��8�Ŋ�����ꍇ���l����Əꍇ��������ςȂ̂ŁA�]�����F�u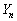 ��8�Ŋ����Ȃ��v�����l���邱�Ƃɂ��܂��B
��8�Ŋ����Ȃ��v�����l���邱�Ƃɂ��܂��B 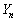 ��8�Ŋ����Ȃ��̂́A�ȉ���3�̏ꍇ�ł��B
��8�Ŋ����Ȃ��̂́A�ȉ���3�̏ꍇ�ł��B(i) n�ׂĊ��1�C3���o���ꍇ�A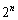 �ʂ�B
�ʂ�B (ii) 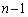 ����1�C3���o���A1��2�܂���4���o���ꍇ�A2�܂���4��n��̎��s�̂ǂ̉�Ŕ����o������n�ʂ肠��A
����1�C3���o���A1��2�܂���4���o���ꍇ�A2�܂���4��n��̎��s�̂ǂ̉�Ŕ����o������n�ʂ肠��A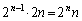 �ʂ�B
�ʂ�B (iii) 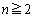 �̂Ƃ��A
�̂Ƃ��A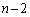 ����1�C3���o���A2��2���o���ꍇ�A2��n��̎��s�̂ǂ�2��Ŕ����o������
����1�C3���o���A2��2���o���ꍇ�A2��n��̎��s�̂ǂ�2��Ŕ����o������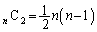 �ʂ肠��A
�ʂ肠��A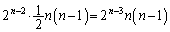 �ʂ�B
�ʂ�B ����āA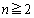 �̂Ƃ��A
�̂Ƃ��A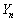 ��8�Ŋ����Ȃ��ꍇ�̐��́A
��8�Ŋ����Ȃ��ꍇ�̐��́A 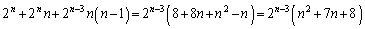 �@����C
�@����C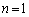 �̂Ƃ��́A1�`4�̂ǂ̐������o���Ă�8�Ŋ���ꂸ�A
�̂Ƃ��́A1�`4�̂ǂ̐������o���Ă�8�Ŋ���ꂸ�A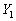 ��8�Ŋ����Ȃ��ꍇ�̐���4�ʂ�ł����A�C��
��8�Ŋ����Ȃ��ꍇ�̐���4�ʂ�ł����A�C��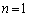 �Ƃ����4�ɂȂ�̂ŁA���ׂĂ�n�ɂ��ćC�Ƃ���OK�ł��B
�Ƃ����4�ɂȂ�̂ŁA���ׂĂ�n�ɂ��ćC�Ƃ���OK�ł��B
�S���ۂ̏ꍇ�̐���(1)�Ɠ��l��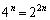 �ʂ�ŁA���߂�m���́A
�ʂ�ŁA���߂�m���́A ......[��]
......[��]
�NjL�D��L(1)�́A��ʓI�ɁA�u1����k�܂Ő����������ꂽk���̃J�[�h����1�����o���Č��ɖ߂����s��n��J��Ԃ��Ƃ��A�����o���������̘a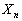 ��
��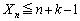 �ƂȂ�m�������߂�B�v�Ƃ������ɂ��Ή��ł���悤�ȕ��j�ōl���܂����B�ł����A��ʐ����̂ĂāA
�ƂȂ�m�������߂�B�v�Ƃ������ɂ��Ή��ł���悤�ȕ��j�ōl���܂����B�ł����A��ʐ����̂ĂāA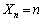 �ƂȂ�ꍇ(n�ׂ�1)�A
�ƂȂ�ꍇ(n�ׂ�1)�A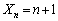 �ƂȂ�ꍇ(
�ƂȂ�ꍇ(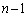 ��1��1��2)�A
��1��1��2)�A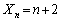 �ƂȂ�ꍇ(
�ƂȂ�ꍇ(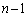 ��1��1��3�ɂȂ邩�A�܂��́A
��1��1��3�ɂȂ邩�A�܂��́A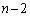 ��1��2��2��o��)�A
��1��2��2��o��)�A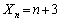 �ƂȂ�ꍇ(
�ƂȂ�ꍇ(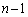 ��1��1��4�ɂȂ邩�A�܂��́A
��1��1��4�ɂȂ邩�A�܂��́A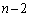 ��1��2�C3��1�o�邩�A�܂��́A
��1��2�C3��1�o�邩�A�܂��́A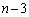 ��1��2��3��o��)�A�e�ꍇ�̐��𐔂��グ��A���}�ɉł��܂�(���̕������Ղ�)�B
��1��2��3��o��)�A�e�ꍇ�̐��𐔂��グ��A���}�ɉł��܂�(���̕������Ղ�)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B