一橋大学2008年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] kを正の整数とする。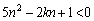
をみたす整数nが、ちょうど1個であるようなkをすべて求めよ。
[解答へ]
[2] 3次方程式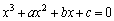
は異なる3つの解p，q，rをもつ。さらに、
，
，
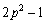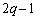も同じ方程式の異なる3つの解である。a，b，c，p，q，rの組をすべて求めよ。
[解答へ]
[3] aを正の実数とする。点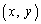
が、不等式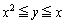
の定める領域を動くとき、常に
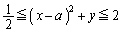となる。aの値の範囲を定めよ。
[解答へ]
[4] 正四面体OABCの1辺の長さを1とする。辺OAを2：1に内分する点をP，辺OBを1：2に内分する点をQとし、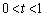
をみたすtに対して、辺OCをt：
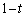に内分する点をRとする。
(1) PQの長さを求めよ。
(2) 
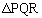の面積が最小となるときのtの値を求めよ。
[解答へ]
[5] nを3以上の整数とする。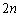
枚のカードがあり、そのうち赤いカードの枚数は6，白いカードの枚数は
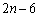である。これら
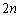枚のカードを、箱Aと箱Bにn枚ずつ無作為に入れる。2つの箱の少なくとも一方に赤いカードがちょうどk枚入っている確率を
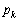とする。
(1) 
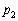をnの式で表せ。さらに、
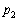を最大にするnをすべて求めよ。
(2) 
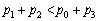をみたすnをすべて求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。