一橋大学2010年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 実数p,q,rに対して、3次多項式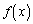 を
を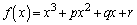 と定める。実数a,c,および0でない実数bに対して、
と定める。実数a,c,および0でない実数bに対して、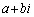 とcはいずれも方程式
とcはいずれも方程式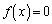 の解であるとする。ただし、iは虚数単位を表す。
の解であるとする。ただし、iは虚数単位を表す。
(1) 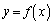 のグラフにおいて、点
のグラフにおいて、点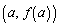 における接線の傾きを
における接線の傾きを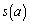 とし、点
とし、点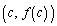 における接線の傾きを
における接線の傾きを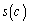 とする。
とする。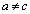 のとき、
のとき、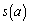 と
と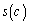 の大小を比較せよ。
の大小を比較せよ。 (2) さらに、a,cは整数であり、bは0でない整数であるとする。次を証明せよ。
(i) p,q,rはすべて整数である。
(ii) pが2の倍数であり、qが4の倍数であるならば、a,b,cはすべて2の倍数である。
[解答へ]
[2] aを実数とする。傾きがmである2つの直線が、曲線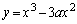 とそれぞれ点A,点Bで接している。
とそれぞれ点A,点Bで接している。
(1) 線分ABの中点をCとすると、Cは曲線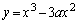 上にあることを示せ。
上にあることを示せ。 (2) 直線ABの方程式が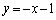 であるとき、a,mの値を求めよ。
であるとき、a,mの値を求めよ。 [解答へ]
[3] 原点をOとするxyz空間内で、x軸上の点A,xy平面上の点B,z軸上の点Cを、次をみたすように定める。
ただし、Aのx座標,Bのy座標,Cのz座標はいずれも正であるとする。さらに、△ABC内の点のうち、Oからの距離が最小の点をHとする。また、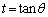 とおく。
とおく。
(1) 線分OHの長さをtの式で表せ。
(2) Hのz座標をtの式で表せ。
[解答へ]
[4] 0以上の整数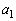 ,
,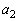 が与えられたとき、数列
が与えられたとき、数列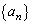 を
を
により定める。
(2) 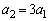 のとき、
のとき、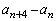 は10の倍数であることを示せ。
は10の倍数であることを示せ。 [解答へ]
[5] nを3以上の自然数とする。サイコロをn回投げ、出た目の数をそれぞれ順に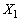 ,
,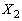 ,・・・,
,・・・,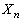 とする。
とする。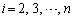 に対して
に対して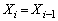 となる事象を
となる事象を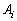 とする。
とする。
(1) 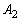 ,
,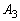 ,・・・,
,・・・,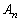 のうち少なくとも1つが起こる確率
のうち少なくとも1つが起こる確率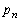 を求めよ。
を求めよ。 (2) 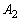 ,
,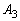 ,・・・,
,・・・,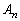 のうち少なくとも2つが起こる確率
のうち少なくとも2つが起こる確率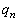 を求めよ。
を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。