�ꋴ�吔�w'10�N�O��[1]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
����p�Cq�Cr�ɑ��āA3��������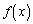 ��
��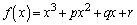 �ƒ�߂�B����a�Cc�C�����0�łȂ�����b�ɑ��āA
�ƒ�߂�B����a�Cc�C�����0�łȂ�����b�ɑ��āA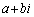 ��c�͂������������
��c�͂������������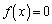 �̉��ł���Ƃ���B�������Ai�͋����P�ʂ�\���B
�̉��ł���Ƃ���B�������Ai�͋����P�ʂ�\���B
(1) 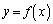 �̃O���t�ɂ����āA�_
�̃O���t�ɂ����āA�_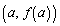 �ɂ�����ڐ��̌X����
�ɂ�����ڐ��̌X����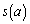 �Ƃ��A�_
�Ƃ��A�_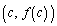 �ɂ�����ڐ��̌X����
�ɂ�����ڐ��̌X����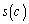 �Ƃ���B
�Ƃ���B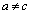 �̂Ƃ��A
�̂Ƃ��A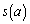 ��
��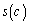 �̑召���r����B
�̑召���r����B (2) ����ɁAa�Cc�͐����ł���Ab��0�łȂ������ł���Ƃ���B�����ؖ�����B
(i) p�Cq�Cr�͂��ׂĐ����ł���B
(ii) p��2�̔{���ł���Aq��4�̔{���ł���Ȃ�Aa�Cb�Cc�͂��ׂ�2�̔{���ł���B
���@�ꋴ��ł͒�Ԃ�3���������E�����̗Z�����ł��B�Ȃ��A�������Q�Ƃ��Ă��������B
(1) 3��������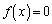 �͎����W���̕������Ȃ̂ŁA
�͎����W���̕������Ȃ̂ŁA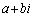 �����ɂȂ�A�������f��
�����ɂȂ�A�������f��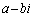 �����ɂȂ�܂�(�������������Q��)�B�܂�A3��������
�����ɂȂ�܂�(�������������Q��)�B�܂�A3��������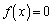 �́A3�̉��A
�́A3�̉��A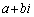 �C
�C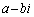 �Cc�������܂��B
�Cc�������܂��B 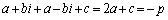 �@����@
�@����@
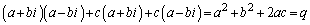 �@����A
�@����A
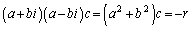 �@����B
�@����B
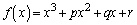
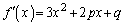 �@(�������Q��)
�@(�������Q��)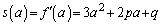 �@(�ڐ����Q��)
�@(�ڐ����Q��)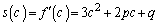
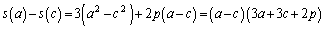
�@��p����ƁA
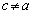 �Ȃ̂ŁA
�Ȃ̂ŁA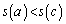 ......[��]
......[��]
(2)(i) �������m�̘a�A���A�ς͐����Ȃ̂ŁA�@�C�A�C�B���Aa�Cb�Cc�������ł���Ap�Cq�Cr�������ł��B(�ؖ��I)
(ii) k�Cl�𐮐��Ƃ��āAp�Cq�́A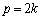 �C
�C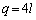 �Ə����܂��B
�Ə����܂��B �@���A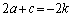
�� 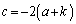 ������Ac��2�̔{���ł��Bm�𐮐��Ƃ��āA
������Ac��2�̔{���ł��Bm�𐮐��Ƃ��āA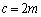 �Ə����܂��B
�Ə����܂��B
�A���A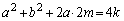
�� 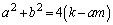 ����āA
����āA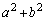 ��4�̔{���ł��Ba�Cb���Ƃ���2�̔{���ł��邱�Ƃ��w���@�ɂ�莦���܂��Ba�Cb���Ƃ���2�̔{���ł��邱�Ƃ�ے肷��ƁA
��4�̔{���ł��Ba�Cb���Ƃ���2�̔{���ł��邱�Ƃ��w���@�ɂ�莦���܂��Ba�Cb���Ƃ���2�̔{���ł��邱�Ƃ�ے肷��ƁA (a) a�Cb�̂ǂ��炩�������ő����͋����B
(b) a�Cb�̂ǂ������B
��2�ʂ�̏ꍇ������܂��B
(a)�ł́Aa�Cb�̂ǂ��炩�������ő������������Ƃ���ƁA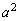 �C
�C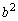 �͂ǂ��炩�������ő����͋����ł��B���̂Ƃ��A
�͂ǂ��炩�������ő����͋����ł��B���̂Ƃ��A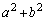 �͊�ƂȂ�A4�̔{���ɂȂ蓾�܂���B
�͊�ƂȂ�A4�̔{���ɂȂ蓾�܂���B (b)�ł́Aj�Cn�𐮐��Ƃ��āA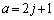 �C
�C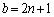 �Ə�����̂ŁA
�Ə�����̂ŁA �ƂȂ�A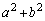 ��4�Ŋ����2�]�鐮���ŁA4�̔{���ɂȂ蓾�܂���B
��4�Ŋ����2�]�鐮���ŁA4�̔{���ɂȂ蓾�܂���B
����āAa�Cb���Ƃ���2�̔{���ł��邱�Ƃ�ے肵������͌��ŁAa�Cb�͂Ƃ���2�̔{���ɂȂ�܂��B �ȏ���Aa�Cb�Cc��2�̔{���ł��B
(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B