�O�p�`�̓��S�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
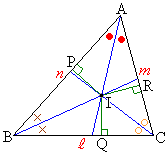
�O�p�`�̊e���p�̓�����1�_�Ō����B���̓_�����S�ƌ����B
�ؖ��@
�O�p�`ABC�� �̓����C
�̓����C �̓����̌�_��I�Ƃ��AI����AB�CBC�CCA�ɐ���IP�CIQ�CIR�����낵�܂��B
�̓����̌�_��I�Ƃ��AI����AB�CBC�CCA�ɐ���IP�CIQ�CIR�����낵�܂��B
 �C
�C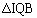 �ɂ����āA
�ɂ����āA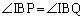 �C
�C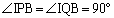 �CIB���ʁA���A
�CIB���ʁA���A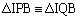
�� 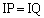 �@����@
�@����@
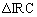 �C
�C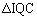 �ɂ����āA
�ɂ����āA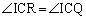 �C
�C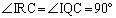 �CIC���ʁA���A
�CIC���ʁA���A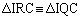
�� 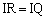 �@����A
�@����A
�@�C�A���A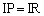
����ƁA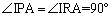 �CIA���ʂ��A
�CIA���ʂ��A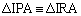
�� 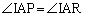
����āAIA��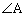 �̓����ł����āA
�̓����ł����āA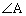 �̓����A
�̓����A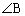 �̓����C
�̓����C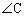 �̓�����1�_I�Ō����܂��B
�̓�����1�_I�Ō����܂��B
�O�p�`ABC��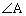 �̓����ƑΕ�BC�̌�_��D�Ƃ���ƁABD�FDC = AB�FAC�@���(��)�ł��邱�Ƃ��m���Ă��܂��B
�̓����ƑΕ�BC�̌�_��D�Ƃ���ƁABD�FDC = AB�FAC�@���(��)�ł��邱�Ƃ��m���Ă��܂��B
������A��L�����ʃx�N�g����p���Ĉȉ��̂悤�Ɏ������Ƃ��ł��܂��B
�O�p�`ABC�� �̓����C
�̓����C �̓����ƑΕ�CA�CAB�Ƃ̌�_��E�CF�C�܂��ABE��CF�̌�_��I�Ƃ��āAAI�̉�����BC�Ƃ̌�_��D�Ƃ��܂��B
�̓����ƑΕ�CA�CAB�Ƃ̌�_��E�CF�C�܂��ABE��CF�̌�_��I�Ƃ��āAAI�̉�����BC�Ƃ̌�_��D�Ƃ��܂��B
�e�ӂ̒������A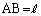 �C
�C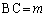 �C
�C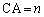 �Ƃ��āA
�Ƃ��āA
(��)���A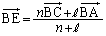 (�x�N�g���̓����E�O�����Q��)
(�x�N�g���̓����E�O�����Q��)
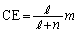 ���ABI�FIE =
���ABI�FIE = 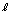 �F
�F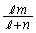 �C����āA
�C����āA
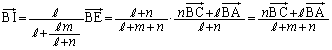 �@����B
�@����B
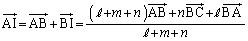
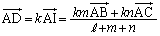 �@����C�@�Ƃ��āAD����AB��̓_�ł��邱�Ƃ���A
�@����C�@�Ƃ��āAD����AB��̓_�ł��邱�Ƃ���A
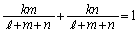 �@(�����������Q��)
�@(�����������Q��)
�� 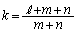
�C�ɑ�����āA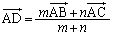
����́A(��)���AD��BC��n�Fm�ɓ�������_�ł��邱�Ƃ��Ӗ����܂�(�x�N�g���̓����E�O�����Q��)�B����āAAD��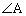 �̓����ł��B
�̓����ł��B
�Ȃ��A�B���ɁA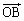 �������āA�e���_�̈ʒu�x�N�g��(�x�N�g����1���Ɨ����Q��)��p���ĕ\���������ƁA
�������āA�e���_�̈ʒu�x�N�g��(�x�N�g����1���Ɨ����Q��)��p���ĕ\���������ƁA
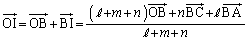
������A�O�p�`ABC�̓��S�̈ʒu�x�N�g�����e�ӂ̒�����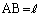 �C
�C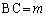 �C
�C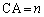 �Ƃ��āA�e���_�̈ʒu�x�N�g����p���āA
�Ƃ��āA�e���_�̈ʒu�x�N�g����p���āA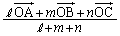 �Ƃ��ꂢ�Ȍ`�ɕ\�����Ƃ��ł��܂��B
�Ƃ��ꂢ�Ȍ`�ɕ\�����Ƃ��ł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 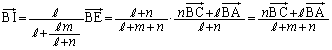 �@����B
�@����B