�c�嗝�H���w'02�N[B1]
���ʂ��ɂ��A���ꂼ��̕������~���̑��ʂ̈ꕔ�ŋߎ����邱�Ƃɂ���āA���̕\�ʐς����߂邱�Ƃ��l����B
(1) ���ar (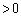 )�̔��~S�F
)�̔��~S�F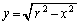 �ƒ���
�ƒ���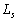 �F
�F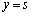 (
(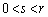 )��2�̌�_�����B���ꂼ��̌�_�ɂ����锼�~S��2�{�̐ڐ��͓_
)��2�̌�_�����B���ꂼ��̌�_�ɂ����锼�~S��2�{�̐ڐ��͓_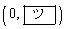 �Ō����B����2�{�̐ڐ��ƒ���
�Ō����B����2�{�̐ڐ��ƒ���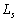 �ň͂܂ꂽ�O�p�`��y���̂܂���1��]���Ăł���~���̑��ʐς�
�ň͂܂ꂽ�O�p�`��y���̂܂���1��]���Ăł���~���̑��ʐς� �ł���B����ɁA���̉~�����畽��
�ł���B����ɁA���̉~�����畽��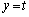 (
( )����ɂ��镔������菜�������̐}�`�̑��ʐς�
)����ɂ��镔������菜�������̐}�`�̑��ʐς� �ł���B
�ł���B (2) n�����R���Ƃ��A �Ƃ���B(1)�Œ�`���ꂽ���̐}�`�ŁA
�Ƃ���B(1)�Œ�`���ꂽ���̐}�`�ŁA �C
�C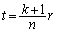 �̂Ƃ��̑��ʐς�
�̂Ƃ��̑��ʐς� �ƕ\���ƁA
�ƕ\���ƁA �ƂȂ�B
(3)  ���ؖ����Ȃ����B
���ؖ����Ȃ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{�����[�����_�̖��Ȃ̂ŁA�����ɋ}���Ȃ��Ɖ�����܂���B
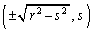 �ɂ�����S���ڐ��́A
�ɂ�����S���ڐ��́A
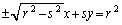 �@(�����܂ŕ�������)�����Ńv���X�Ƃ������ƃ}�C�i�X�Ƃ�������A�����ĉ����ƁA
�@(�����܂ŕ�������)�����Ńv���X�Ƃ������ƃ}�C�i�X�Ƃ�������A�����ĉ����ƁA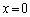 �C
�C
2�{�̐ڐ��͓_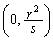 �Ō����܂��B
�Ō����܂��B 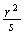 ......[��]
......[��](�e) �~���̒�ʂ̔��a�� �C��ʂ̉~���̒�����
�C��ʂ̉~���̒�����
�~���̗Ő��̒���R��
�~���̑��ʂ�W�J���Ăł����`(���S�p��θ �Ƃ��܂�)�̌ʂ̒����ƒ�ʂ̉~���̒����͓������A
�� 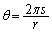 �~���̑��ʐ�
�~���̑��ʐ�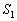 �́A
�́A 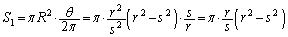
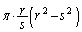 ......[��]
......[��](�g) ���̉~���̕��� �����ɂ��镔���̗Ő��̒���
�����ɂ��镔���̗Ő��̒���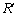 �́A
�́A ���A
�~�����畽�� ����ɂ��镔������菜�������̐}�`�̑��ʐ�
����ɂ��镔������菜�������̐}�`�̑��ʐ� �́A
�́A 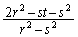 ......[��]
......[��]
(2)(�i) (�g)�̌��ʂ�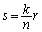 �C
�C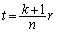 ��������ƁA���ʐ�
��������ƁA���ʐ�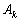 �́A
�́A 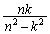 ......[��]
......[��]
(3) 
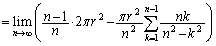
 �@����@
�@����@�����ŁA�敪���ϖ@�̋Z�I���g���đ�2�����A �Ƃ��Ă��܂��ƁA
�Ƃ����Ƃ��ɁA ��x��1�����ł��Ȃ��č���܂��B
��x��1�����ł��Ȃ��č���܂��B
�@�ŁA���ɁA �̌`�͌����Ă���̂ŁA
�̌`�͌����Ă���̂ŁA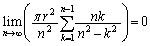 �������Ηǂ��킯�ł����A
�������Ηǂ��킯�ł����A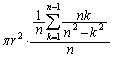 �̌`�ɂ��Ă��܂��ƁA����
�̌`�ɂ��Ă��܂��ƁA���� �C���q
�C���q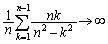 �ƂȂ��Ă��܂��Ȃ��̂ł��B
�ƂȂ��Ă��܂��Ȃ��̂ł��B
�����ŁA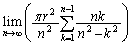 �����������ό`���邱�Ƃɂ��܂��B
�����������ό`���邱�Ƃɂ��܂��B �����ŁA���̒��ɂ���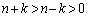 �C
�C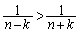 ���A
���A 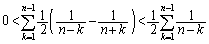 �@����A
�@����A
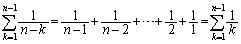 �ƂȂ�̂ŁA�K�i�^�O���t�̖ʐς̋Z�I���g���܂��B�E�}�ɂ����āA
�ƂȂ�̂ŁA�K�i�^�O���t�̖ʐς̋Z�I���g���܂��B�E�}�ɂ����āA �͉��F���F�����̖ʐςŁA�K�i�^�O���t���Ȑ�
�͉��F���F�����̖ʐςŁA�K�i�^�O���t���Ȑ� �ƋȐ�
�ƋȐ� �ɂ͂��܂�邱�Ƃ���A
�ɂ͂��܂�邱�Ƃ���A�� 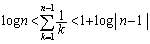 �e�ӂ�n�Ŋ����āA
�e�ӂ�n�Ŋ����āA �����ŁA �̂Ƃ��A
�̂Ƃ��A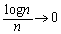 ���A���Ӂ�0�C�E�Ӂ�0�͂��݂����̌������A
���A���Ӂ�0�C�E�Ӂ�0�͂��݂����̌������A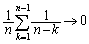
�A�̊e�ӂ�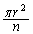 �������āA
�������āA  �̂Ƃ��A�E�Ӂ�0�Ȃ̂ŁA�͂��݂����̌������A
�̂Ƃ��A�E�Ӂ�0�Ȃ̂ŁA�͂��݂����̌������A
���ǁA�@�̑�2���̋Ɍ��ɂ��āA�@���A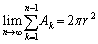 �@(�ؖ��I)
�@(�ؖ��I) ���D�r���ɏo�Ă����A�g �̂Ƃ��A
�̂Ƃ��A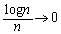 �h�ɂ��ẮA�ȉ��̂悤�ɂ��Ď����܂��B
�h�ɂ��ẮA�ȉ��̂悤�ɂ��Ď����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
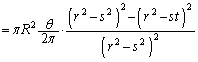


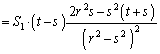
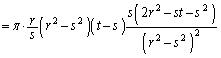 �@(�� (�e))
�@(�� (�e))

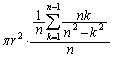 �̌`�ɂ��Ă��܂��ƁA����
�̌`�ɂ��Ă��܂��ƁA����