慶應大学理工学部2005年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[A1] 空間内のxy平面上において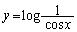
(
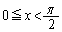)で表される曲線をCとする。C上の点P
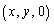をとり、原点からPまでの曲線の長さをsとする。空間内でPの真上に点Q
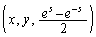をとる。
(1) 曲線の長さsをxの関数として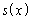
で表す。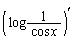
＝ ア であり、また
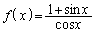とおくと、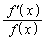
＝ イ であるから、
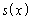＝ ウ となる。したがって、線分PQの長さはxの関数
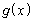となり、特に
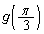＝ エ である。 (2) 点Pからx軸へおろした垂線の足をR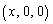
とし、PQとPRを2辺とする長方形を
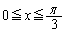の範囲で動かして立体をつくる。このとき、この立体の体積は オ である。 [解答へ]
[A2] 点Pが数直線上の整数点(座標が整数である点)を次の規則にしたがって正の方向に移動していく。
(i) 最初の時点でのPの座標は0である(Pは原点Oの上にある)。
(ii) ある時点でのPの座標がkのとき、次の時点でPは座標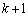
の点か、または座標
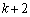の点のどちらかに、それぞれ
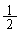の確率で移動する。 正の整数nに対して、ある時点でPの座標がnとなる確率(すなわち、Pが座標nの点を飛びこえてしまわない確率)を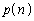
で表す。たとえば、
，
，
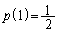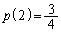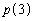＝ カ ，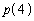
＝ キ である。すると、
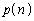は漸化式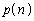
＝ ク をみたす。したがって、
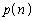をnの式で表すと ケ となり、
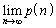＝ コ である。
[解答へ]
[A3] 平面上に4点K，E，I，Oがある。Kは動点で、その座標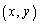
が時刻t (
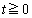)の関数として
，
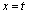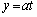で与えられている(aは正の実数)。E
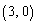，I
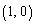，O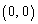
は定点である。2点E，Iを通り、直線
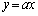に第1象限で接する円の中心の座標は( サ ， シ )である。円周角の性質から、
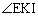が最大となるのはt＝ ス のときである。そのときの線分OKの長さ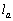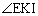を
，
を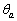
とするとき、
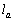＝ セ ，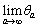
＝ ソ である。
[解答へ]
[B1] 2行2列の行列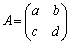
，
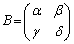を考える。Aにおいて、bとcを入れかえた行列を
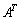で表す。すなわち、
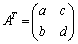である。同様に、
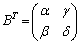とおく。以下で、Bはつねに
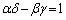をみたすものとする。
(1) 
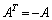となるための必要十分条件は
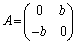であることを証明しなさい。 (2) 
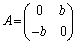のとき、すべてのBに対して
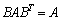となることを証明しなさい。 (3) すべてのBに対して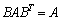
が成り立つならば、
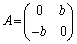であることを証明しなさい。 [解答へ]
[B2] 実数tに対して空間の点P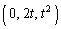
を定め、Pと点A
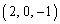を結ぶ線分PAがxy平面と交わる点をQ
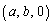とする。
(1) このときa，bをtで表し、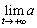
，
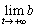を求めなさい。 (2) tが実数全体を動くとき、Qの軌跡を求めなさい。また軌跡の概形をxy平面上に描きなさい。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。