�c�嗝�H���w'05�N[B1]
2�s2��̍s��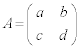 �C
�C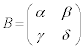 ���l����BA�ɂ����āAb��c����ꂩ�����s���
���l����BA�ɂ����āAb��c����ꂩ�����s���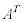 �ŕ\���B���Ȃ킿�A
�ŕ\���B���Ȃ킿�A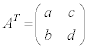 �ł���B���l�ɁA
�ł���B���l�ɁA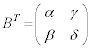 �Ƃ����B�ȉ��ŁAB�͂˂�
�Ƃ����B�ȉ��ŁAB�͂˂�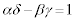 ���݂������̂Ƃ���B
���݂������̂Ƃ���B
(1) 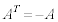 �ƂȂ邽�߂̕K�v�\��������
�ƂȂ邽�߂̕K�v�\��������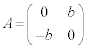 �ł��邱�Ƃ��ؖ����Ȃ����B
�ł��邱�Ƃ��ؖ����Ȃ����B (2) 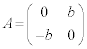 �̂Ƃ��A���ׂĂ�B�ɑ���
�̂Ƃ��A���ׂĂ�B�ɑ���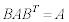 �ƂȂ邱�Ƃ��ؖ����Ȃ����B
�ƂȂ邱�Ƃ��ؖ����Ȃ����B (3) ���ׂĂ�B�ɑ���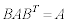 �����藧�Ȃ�A
�����藧�Ȃ�A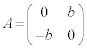 �ł��邱�Ƃ��ؖ����Ȃ����B
�ł��邱�Ƃ��ؖ����Ȃ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@A�ɑ���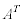 ��A�̓]�u�s��ƌ����܂��B�Ȃ��A�s�����Q�Ƃ��Ă��������B
��A�̓]�u�s��ƌ����܂��B�Ȃ��A�s�����Q�Ƃ��Ă��������B
(1) 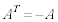 �̂Ƃ��A
�̂Ƃ��A ����āA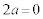 �C
�C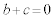 �C
�C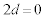
�� 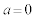 �C
�C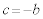 �C
�C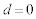
�t�ɁA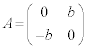 �̂Ƃ��A
�̂Ƃ��A 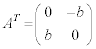 �C
�C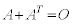
�� 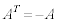 �@(�ؖ��I)
�@(�ؖ��I)
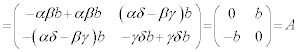 �@(�ؖ��I)
�@(�ؖ��I)
(3) 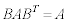 �̗��ӂ̍�����
�̗��ӂ̍�����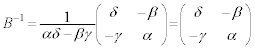 ��������(�t�s�����Q��)�ƁA
��������(�t�s�����Q��)�ƁA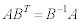 ���A
���A 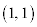 �������ׂāA
�������ׂāA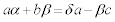 ����@
����@
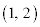 �������ׂāA
�������ׂāA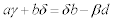 ���A
���A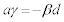 ����A
����A
�@���A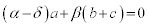
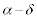 �Cβ �͔C�ӂ̎������Ƃ邩��A
�Cβ �͔C�ӂ̎������Ƃ邩��A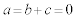 (�P�����̏���)��
(�P�����̏���)�� 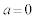 �C
�C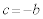
�A���Aβ �Cγ ���C�ӂ̎������Ƃ邩��A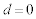
�� 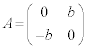 �@(�ؖ��I)
�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 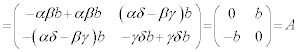 �@(�ؖ��I)
�@(�ؖ��I)