�c�嗝�H���w'05�N[A3]
���ʏ��4�_K�CE�CI�CO������BK�͓��_�ŁA���̍��W ������t (
������t ( )�̊��Ƃ���
)�̊��Ƃ���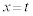 �C
�C �ŗ^�����Ă���(a�͐��̎���)�BE
�ŗ^�����Ă���(a�͐��̎���)�BE �CI
�CI �CO
�CO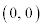 �͒�_�ł���B2�_E�CI��ʂ�A����
�͒�_�ł���B2�_E�CI��ʂ�A����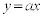 �ɑ�1�ی��Őڂ���~�̒��S�̍��W��(�@�T�@�C�@�V�@)�ł���B�~���p�̐�������A
�ɑ�1�ی��Őڂ���~�̒��S�̍��W��(�@�T�@�C�@�V�@)�ł���B�~���p�̐�������A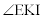 ���ő�ƂȂ�̂�t���@�X�@�̂Ƃ��ł���B���̂Ƃ��̐���OK�̒�����
���ő�ƂȂ�̂�t���@�X�@�̂Ƃ��ł���B���̂Ƃ��̐���OK�̒�����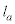 �C
�C ��
�� �Ƃ���Ƃ��A
�Ƃ���Ƃ��A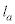 ���@�Z�@�C
���@�Z�@�C ���@�\�@�ł���B
���@�\�@�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ���@(�T)(�V) 2�_E�CI��ʂ�~�̒��SC�͐���EI�̐���2�������F
���@(�T)(�V) 2�_E�CI��ʂ�~�̒��SC�͐���EI�̐���2�������F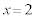 ��ɂ���܂��BC�̍��W��
��ɂ���܂��BC�̍��W�� �ƕ\���܂��B
�ƕ\���܂��B�~�ƒ��� ���ڂ���̂ŁA�~�̒��SC
���ڂ���̂ŁA�~�̒��SC ��
��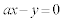 �Ƃ̋����́A���a�A�����A
�Ƃ̋����́A���a�A�����A �ɓ�����(�~�ƒ����̈ʒu�W�Q��)�A
�ɓ�����(�~�ƒ����̈ʒu�W�Q��)�A ��������ӂ�2�悷��ƁA
�������āA
 �@(
�@( )
)�� 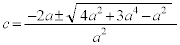
2���̂����A��1�ی��Őڂ���̂́}���{�̕��ŁA  ����@
����@���߂�~�̒��S�̍��W�́A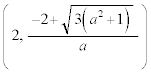 ......[��]
......[��]
(�X) ����EK��(1)�̉~�Ƃ̌�_��D�Ƃ���ƁAK�͉~����܂��͉~�̊O���̓_�Ȃ̂ŁA
�����ŁA�����EI�̏�ɗ��~���p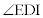 �͈��ŁA��������������(
�͈��ŁA��������������( ���ő�)�̂́AK���~����̓_�̂Ƃ��ŁA�����Ȃ�̂́AK������
���ő�)�̂́AK���~����̓_�̂Ƃ��ŁA�����Ȃ�̂́AK������ �Ɖ~�Ƃ̐ړ_�ɂȂ�Ƃ��ł��B
�Ɖ~�Ƃ̐ړ_�ɂȂ�Ƃ��ł��B
�]���āA�~�̒��SC ��ʂ蒼��
��ʂ蒼�� �Ɛ����Ȓ���m�ƁA
�Ɛ����Ȓ���m�ƁA �Ƃ̌�_�����߂�悭�A
�Ƃ̌�_�����߂�悭�A
����m�F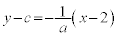 �@(2�����̕��s�E�������Q��)
�@(2�����̕��s�E�������Q��) �ƘA�����āA
�ƘA�����āA �� 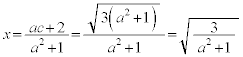 (�@���g����c������)���̂Ƃ���t�̒l���A
(�@���g����c������)���̂Ƃ���t�̒l���A .......[��]
.......[��]
(�Z) ���̂Ƃ��AK����x���ɉ��낵�������̑���H�Ƃ���ƁAKH�FOH��a�F1���A
OH�FOK��1�F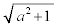
��  ......[��]������A
......[��]������A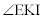 �̍ő�l��^����_K�́A���_�𒆐S�Ƃ��锼�a
�̍ő�l��^����_K�́A���_�𒆐S�Ƃ��锼�a �̉~��
�̉~�� ��ɂ��邱�Ƃ��킩��܂��B ����A
��ɂ��邱�Ƃ��킩��܂��B ����A 
(�\) 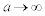 �̂Ƃ��A����
�̂Ƃ��A���� ��y���ɋ߂Â��܂��B
��y���ɋ߂Â��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ����@
����@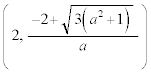 ......[��]
......[��]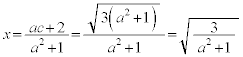 (�@���g����c������)
(�@���g����c������)