�c�嗝�H���w'05�N[A2]
�_P����������̐����_(���W�������ł���_)�����̋K���ɂ��������Đ��̕����Ɉړ����Ă����B
(i) �ŏ��̎��_�ł�P�̍��W��0�ł���(P�͌��_O�̏�ɂ���)�B
(ii) ���鎞�_�ł�P�̍��W��k�̂Ƃ��A���̎��_��P�͍��W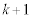 �̓_���A�܂��͍��W
�̓_���A�܂��͍��W �̓_�̂ǂ��炩�ɁA���ꂼ��
�̓_�̂ǂ��炩�ɁA���ꂼ��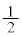 �̊m���ňړ�����B
�̊m���ňړ�����B ���̐���n�ɑ��āA���鎞�_��P�̍��W��n�ƂȂ�m��(���Ȃ킿�AP�����Wn�̓_���т����Ă��܂�Ȃ��m��)��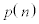 �ŕ\���B���Ƃ��A
�ŕ\���B���Ƃ��A �C
�C �C
�C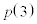 ���@�J�@�C
���@�J�@�C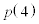 ���@�L�@�ł���B����ƁA
���@�L�@�ł���B����ƁA �͑Q����
�͑Q����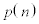 ���@�N�@���݂����B���������āA
���@�N�@���݂����B���������āA ��n�̎��ŕ\�����@�P�@�ƂȂ�A
��n�̎��ŕ\�����@�P�@�ƂȂ�A ���@�R�@�ł���B
���@�R�@�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ���@(�J) �E�̎��`�}�́A�}1�{���m���͂��ׂ�
���@(�J) �E�̎��`�}�́A�}1�{���m���͂��ׂ�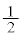
���`�}���A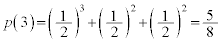 ......[��]�@(�Ɨ����s�̊m�����Q��)
......[��]�@(�Ɨ����s�̊m�����Q��)
(�L) 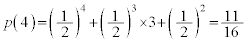 ......[��]
......[��]
(�N) ���Wn�̓_�ɗ���̂́A���W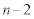 �̓_���璼��n�ɗ��邩�A���W
�̓_���璼��n�ɗ��邩�A���W �̓_����n�ɗ��邩�̂����ꂩ�ŁA���̗��҂��r���ł��B���W
�̓_����n�ɗ��邩�̂����ꂩ�ŁA���̗��҂��r���ł��B���W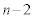 �̓_�C���W
�̓_�C���W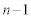 �̓_�ɗ���m���͂��ꂼ��
�̓_�ɗ���m���͂��ꂼ��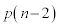 �C
�C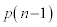 �ł���A��������e�X
�ł���A��������e�X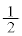 �̊m����n�ɗ���̂ŁA���Wn�ɗ���m��
�̊m����n�ɗ���̂ŁA���Wn�ɗ���m��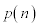 �́A
�́A  ......[��] ����@
......[��] ����@�����3���ԑQ�����ł��B�ʉ��@���Wn�̓_���щz����(�m��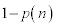 )���ۂ́A���W
)���ۂ́A���W �̓_�ɂ���(�m��
�̓_�ɂ���(�m��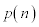 )�Ƃ��Ɋm��
)�Ƃ��Ɋm��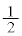 �ŋN����܂��B����āA
�ŋN����܂��B����āA �� 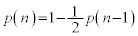 ......[��]�@����C
......[��]�@����C
�Ƃ��邱�Ƃ��ł��܂��B�����2���ԑQ�����ł��B
(�P) �@�̓����������́A
�� 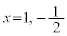 �@ ��
�@ ��  ������A����
������A����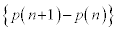 �́A����
�́A���� �C����
�C����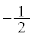 �����䐔���B
�����䐔���B
����āA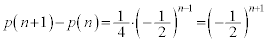 ����A
����A
�@ �� 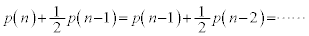
����āA ����B
����B
�B�|�A���A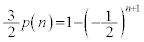
��  ......[��]�ʉ��@(�N)�ŇC�̕����Ƃ����ꍇ�ɂ́A
......[��]�ʉ��@(�N)�ŇC�̕����Ƃ����ꍇ�ɂ́A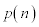 ��
�� ��α�Œu��������1���������A
��α�Œu��������1���������A 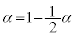 �@����D
�@����D���A
�C�|�D���A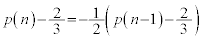
 �́A�����F
�́A�����F �C����F
�C����F �̓��䐔��ŁA
�̓��䐔��ŁA ��  ......[��]�ƂȂ�܂��B
......[��]�ƂȂ�܂��B
(�R) 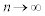 �̂Ƃ�
�̂Ƃ�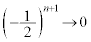 ���A
���A ......[��]�@(����̋Ɍ����Q��)
......[��]�@(����̋Ɍ����Q��)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B