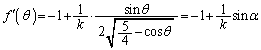慶大理工数学'07年[A3]
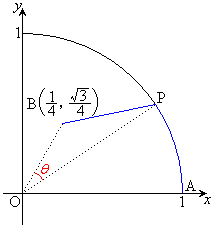 図のように、座標平面上に2点A
図のように、座標平面上に2点A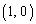 ,B
,B が与えられている。また、原点Oを中心とした半径1の円周上に、
が与えられている。また、原点Oを中心とした半径1の円周上に、 が0以上
が0以上 以下であるような点Pがある。
以下であるような点Pがある。
いま、動点Xが、点Aを出発し、円周に沿って反時計回りに点Pに至り、その後線分PBに沿って点Bに移動する。ただし、円周上では速さ1で移動し、線分PB上では速さk (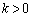 )で移動するものとする。
)で移動するものとする。 (
(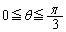 )とし、動点XがAからBへ至る所要時間を
)とし、動点XがAからBへ至る所要時間を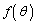 とする。
とする。
(1) 線分PBの長さを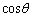 を用いて表すと、 セ となる。
を用いて表すと、 セ となる。 (2)  の導関数は
の導関数は  ソ
ソ となる。
(3)  が
が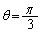 のとき最小となるためには、
のとき最小となるためには、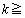 タ となることが必要十分である。
タ となることが必要十分である。 (4)  とおくとき、
とおくとき、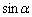 をθ の式で表すと、
をθ の式で表すと、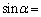 チ となる。
チ となる。 また、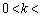 タ とするとき、
タ とするとき、 が最小となるようにθ を選ぶと、αとkの間には、 ツ という関係が成立する。
が最小となるようにθ を選ぶと、αとkの間には、 ツ という関係が成立する。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 慶大理工のよくあるタイプの問題です。以前は、このタイプの問題でもよく練られたおもしろい問題があったんですけどね。
途中の(タ)が、ていねいに調べていると非常に面倒なのですが、空所補充問題なので、試験会場では、詳細な議論を省いて正答しておくのが賢明でしょう。
(1) (セ)  です。右上図より、
です。右上図より、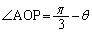 ,円弧APの長さは、
,円弧APの長さは、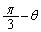 ,円弧APを動点Xが進むのに要する時間は、
,円弧APを動点Xが進むのに要する時間は、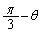
∴ 
 ......[答]
......[答]
(2) (ソ) PBを動点Xが進むのに要する時間は、
(3) (タ) 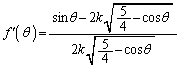
この分母は、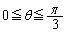 において正です。
において正です。
分子を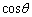 に関する2次関数とみて、
に関する2次関数とみて、 とおくと、
とおくと、 という風に分類します。
(i) 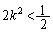 ,つまり、
,つまり、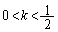 のとき、
のとき、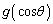 は、
は、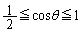 において、
において、 の減少関数で、
の減少関数で、  ,
,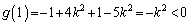
より、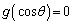 は、
は、 の範囲に解
の範囲に解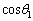 (
(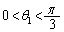 )をもち、
)をもち、
 ,つまり、
,つまり、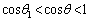 において、
において、 ,
,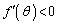 ,
,
 ,つまり、
,つまり、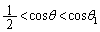 において、
において、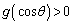 ,
,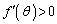
従って、 は
は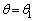 において極小値をもつ(関数の増減を参照)ので、
において極小値をもつ(関数の増減を参照)ので、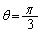 において最小とはならず、不適。注意 上記で、θ→大、のとき、
において最小とはならず、不適。注意 上記で、θ→大、のとき、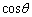 →小、であることに充分に注意してください。
→小、であることに充分に注意してください。
より、
 において、
において、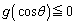 ,
,
従って、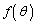 は単調減少で、
は単調減少で、 において最小になります。
において最小になります。
(iii) 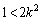 ,つまり、
,つまり、 のとき、
のとき、 は、
は、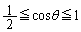 において、
において、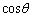 の増加関数で、
の増加関数で、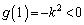 より、
より、 において、
において、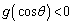 ,
,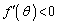
従って、 は単調減少で、
は単調減少で、 において最小になります。
において最小になります。
以上より、 が
が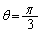 のとき最小となるためには、
のとき最小となるためには、 となることが必要十分です。
となることが必要十分です。  ......[答]
......[答]
(4) (チ) 三角形POBにおいて、正弦定理より、 ∴ 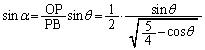 ......[答]
......[答] (ツ) 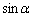 を用いて、
を用いて、 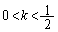 のとき、つまり、(3)(i)のとき、
のとき、つまり、(3)(i)のとき、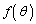 は
は において最小となりますが、このとき、
において最小となりますが、このとき、∴ 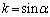 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 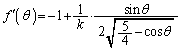
 ......[答]
......[答]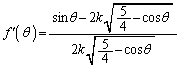
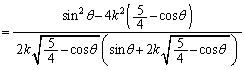
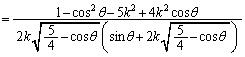
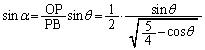 ......[答]
......[答]