�c�嗝�H���w'09�N[B1]
xy���ʏ�ɂ����ĉ~C�F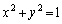 �ƒ���l�F
�ƒ���l�F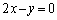 ���l����B
���l����B
(1) �s��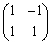 �ŕ\�����1���ϊ��ɂ���āA�~C�͂ǂ̂悤�Ȑ}�`�Ɉڂ邩�B���R�����ē����Ȃ����B
�ŕ\�����1���ϊ��ɂ���āA�~C�͂ǂ̂悤�Ȑ}�`�Ɉڂ邩�B���R�����ē����Ȃ����B (2) �~C�ƒ���l�Ƃ̌�_�̍��W��(�@�q�@�C�@�t�@)�C(�@�w�@�C�@�z�@)�ł���B
(3) �~C���~C�Ɉڂ��A����l��l�Ɉڂ�1���ϊ���\���s��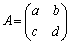 �����ׂċ��߂Ȃ����B���߂�ߒ����������ƁB
�����ׂċ��߂Ȃ����B���߂�ߒ����������ƁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͍s���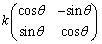 �̌`�ɏ���������ƁA�����v���Ɋpθ��]���Ak�{�̊g����s���ϊ��ł��邱�Ƃ��킩��܂��B
�̌`�ɏ���������ƁA�����v���Ɋpθ��]���Ak�{�̊g����s���ϊ��ł��邱�Ƃ��킩��܂��B
(3)�́A����ϊ��ƌĂ��1���ϊ����������ł��B1���ϊ�(����2)�̒���ϊ��̋L�q���Q�Ƃ��Ă��������B
(1) 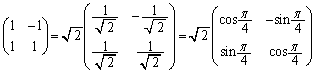
�ŕ\�����1���ϊ��́A�����v���Ɋp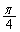 ��]��
��]��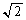 �{�̊g����s���܂��B����āA�~C�͔��a��
�{�̊g����s���܂��B����āA�~C�͔��a��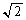 �{�̉~�F
�{�̉~�F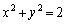 �Ɉڂ�܂��B
�Ɉڂ�܂��B
(2) C�F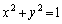 �Cl�F
�Cl�F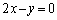
��A�����āA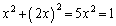
�� 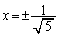 �C
�C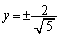 (��������)
(��������)
C��l�̌�_�́A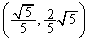 �C
�C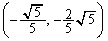 (�q)(�t)(��)(�z)�͏��ɁA
(�q)(�t)(��)(�z)�͏��ɁA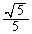 �C
�C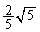 �C
�C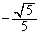 �C
�C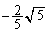 ......[��]
......[��]
(3) A�̕\��1���ϊ�������l�F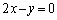 ��̓_
��̓_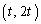 (t �͔C�ӂ̎���)��l��Ɉڂ��̂ŁA
(t �͔C�ӂ̎���)��l��Ɉڂ��̂ŁA 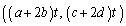 ��l�F
��l�F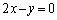 ��̓_�ŁA
��̓_�ŁAt �͔C�ӂ̎����Ȃ̂ŁA
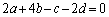 �@����@
�@����@A�̕\��1���ϊ����~C�F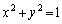 ��̓_
��̓_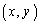 ���~C��Ɉڂ��̂ŁA
���~C��Ɉڂ��̂ŁA 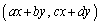 ���~C�F
���~C�F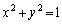 ��̓_�ŁA
��̓_�ŁA���ꂪ�A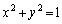 �Ɉ�v���邽�߂ɁAx�Cy�Ɉˑ����Ȃ��萔a�Cb�Cc�Cd�ɂ��āA
�Ɉ�v���邽�߂ɁAx�Cy�Ɉˑ����Ȃ��萔a�Cb�Cc�Cd�ɂ��āA 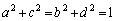 �C
�C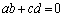 �@(�������Q��)
�@(�������Q��)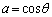 �C
�C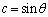 (
(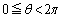 )�Ƃ����ƁA
)�Ƃ����ƁA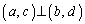 ���A
���A
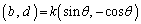 �@(
�@(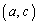 ��x������y���������ւ��Ay�����Ƀ}�C�i�X������k�{����)
��x������y���������ւ��Ay�����Ƀ}�C�i�X������k�{����)�Ƃ����܂����A
�� 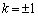 ����āA
����āA 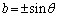 �C
�C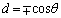 (��������)
(��������)(i) 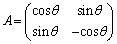 �C(ii)
�C(ii) 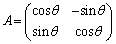 ��2�̏ꍇ������܂��B
��2�̏ꍇ������܂��B (i) 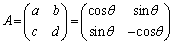 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A 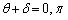 ��
�� 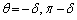
�� 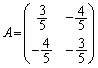
�� 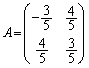
(ii) 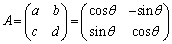 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A �� 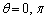
�� 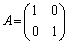
�� 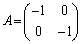
�ȏ���A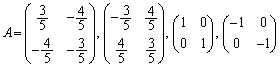 ......[��]���D(2)�𗘗p���āAA�̕\��1���ϊ��ɂ��AC��l�̌�_��C��l�̌�_�Ɉڂ�A�Ƃ��āA�ȉ��̂悤�ɉ��邱�Ƃ��ł��܂��B
......[��]���D(2)�𗘗p���āAA�̕\��1���ϊ��ɂ��AC��l�̌�_��C��l�̌�_�Ɉڂ�A�Ƃ��āA�ȉ��̂悤�ɉ��邱�Ƃ��ł��܂��B
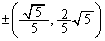 ��A�̕\��1���ϊ����{���ƁA
��A�̕\��1���ϊ����{���ƁA �Ɉڂ�܂����A������܂��A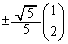 �̐����̂ǂ��炩�Ȃ̂ŁA
�̐����̂ǂ��炩�Ȃ̂ŁA 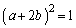 �C
�C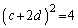 �@����A
�@����A�܂��A�~C��̓_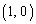 �C
�C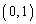 ��A�̕\��1���ϊ��ɂ��A�܂��~C��Ɉڂ�̂ŁA
��A�̕\��1���ϊ��ɂ��A�܂��~C��Ɉڂ�̂ŁA 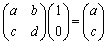 �C
�C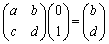
���A
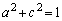 �C
�C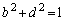 �@����B
�@����B�A�C�B��A�����邱�Ƃɂ��Aa�Cb�Cc�Cd�����߂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 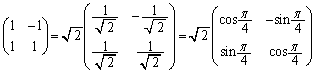
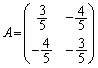
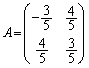
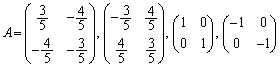 ......[��]
......[��]