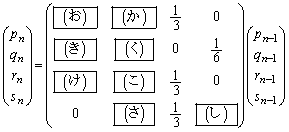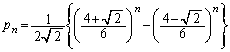Œc‘هˆمگ”ٹw'09”N[3]
ˆب‰؛‚ج•¶ڈح‚ج‹َ—“‚ة“Kگط‚بگ”‚ـ‚½‚حژ®‚ً“ü‚ê‚ؤ•¶ڈح‚ًٹ®گ¬‚³‚¹‚ب‚³‚¢پB‚ـ‚½پAگف–â(3)‚ة“ڑ‚¦‚ب‚³‚¢پB
گ³•ûŒ`‚ج4‚آ‚ج’¸“_‚ة پC
پC پC
پC پC
پC ‚جڈ‡‚ة”½ژŒv‰ٌ‚è‚ة–¼‘O‚ً‚آ‚¯‚éپB
‚جڈ‡‚ة”½ژŒv‰ٌ‚è‚ة–¼‘O‚ً‚آ‚¯‚éپB پC
پC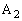 ڈم‚ة‚ح•\‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚«پA
ڈم‚ة‚ح•\‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚«پA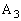 پC
پC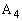 ڈم‚ة‚ح— ‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚پB‚¢‚ـژں‚ج‘€چىT‚ً‰½‰ٌ‚©ŒJ‚è•ش‚µچs‚¤پB
ڈم‚ة‚ح— ‚ًڈم‚ة‚µ‚½چd‰ف‚ً1–‡‚¸‚آ’u‚پB‚¢‚ـژں‚ج‘€چىT‚ً‰½‰ٌ‚©ŒJ‚è•ش‚µچs‚¤پB
‘€چىTپF4‚آ‚ج’¸“_‚ج‚ا‚ê‚©‚ًٹm—¦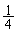 ‚¸‚آ‚إ‘I‚شپB‘I‚خ‚ꂽ’¸“_‚ً ‚¸‚آ‚إ‘I‚شپB‘I‚خ‚ꂽ’¸“_‚ً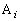
( )‚ئ‚·‚é‚ئ‚«پA•س‚ة‰ˆ‚ء‚ؤ )‚ئ‚·‚é‚ئ‚«پA•س‚ة‰ˆ‚ء‚ؤ ڈم‚جچd‰ف‚ئ•ہ‚ٌ‚إ‚¢‚é ڈم‚جچd‰ف‚ئ•ہ‚ٌ‚إ‚¢‚é
چd‰ف2–‡‚ج‚¤‚؟ ڈم‚جچd‰ف‚ئ‚ح‹t‚ج–ت‚ًڈم‚ة‚µ‚½‚à‚ج‚ج–‡گ”‚ً ڈم‚جچd‰ف‚ئ‚ح‹t‚ج–ت‚ًڈم‚ة‚µ‚½‚à‚ج‚ج–‡گ”‚ً
k‚ئ‚·‚éپBژں‚ةپA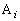 ڈم‚جچd‰ف‚ًٹm—¦ ڈم‚جچd‰ف‚ًٹm—¦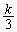 ‚إ‚ذ‚ء‚‚è•ش‚µپAٹm—¦ ‚إ‚ذ‚ء‚‚è•ش‚µپAٹm—¦
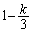 ‚إ‚»‚ج‚ـ‚ـ‚ة‚µ‚ؤ‚¨‚پB ‚إ‚»‚ج‚ـ‚ـ‚ة‚µ‚ؤ‚¨‚پB |
ˆب‰؛پAn‚ًژ©‘Rگ”‚ئ‚·‚éپB‘€چىT‚ًn‰ٌŒJ‚è•ش‚µچs‚ء‚½Œ‹‰تپA•\‚ًڈم‚ة‚µ‚½چd‰ف‚ھ‚؟‚ه‚¤‚ا1–‡‚¾‚¯‚ ‚éٹm—¦‚ً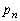 پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ•س‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً
پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ•س‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً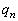 پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ‘خٹpگü‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً
پC‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ‘خٹpگü‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éٹm—¦‚ً پC‚؟‚ه‚¤‚ا3–‡‚¾‚¯‚ ‚éٹm—¦‚ً
پC‚؟‚ه‚¤‚ا3–‡‚¾‚¯‚ ‚éٹm—¦‚ً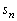 ‚ئ‚·‚éپB
‚ئ‚·‚éپB
(2) 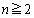 ‚ج‚ئ‚«پA
‚ج‚ئ‚«پA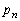 پC
پC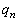 پC
پC پC
پC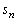 ‚ئ
‚ئ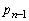 پC
پC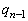 پC
پC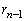 پC
پC ‚جٹضŒW‚ً4ژں‚جگ³•ûچs—ٌ‚ً—p‚¢‚ؤ•\‚·‚ئپA
‚جٹضŒW‚ً4ژں‚جگ³•ûچs—ٌ‚ً—p‚¢‚ؤ•\‚·‚ئپA ‚إ‚ ‚éپB‚±‚ê‚و‚è”Cˆس‚جn‚ة‘خ‚µ‚ؤ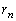 ‚ً‹پ‚ك‚é‚ئ
‚ً‹پ‚ك‚é‚ئ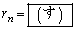 ‚إ‚ ‚éپB
‚إ‚ ‚éپB
(3) ”Cˆس‚جn‚ة‘خ‚µ‚ؤ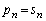 ‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB (4) ”Cˆس‚جn‚ة‘خ‚µ‚ؤ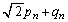 ‚ئ
‚ئ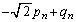 ‚ً‹پ‚ك‚é‚ئپA
‚ً‹پ‚ك‚é‚ئپA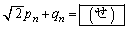 پC
پC ‚إ‚ ‚éپB‚±‚ê‚و‚èپA
‚إ‚ ‚éپB‚±‚ê‚و‚èپA پC
پC ‚إ‚ ‚éپB
‚إ‚ ‚éپB
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
‰ً“ڑپ@‘Jˆعگ}‚ًڈ‘‚¢‚ؤکA—§‘Q‰»ژ®‚ًچى‚éƒ^ƒCƒv‚جٹm—¦‚ج–â‘è‚إ‚·پB‚و‚Œ©‚éƒ^ƒCƒv‚ئ‚حŒ¾‚ء‚ؤ‚àپAˆê‚ذ‚ث‚è“ü‚ء‚ؤ‚¢‚ؤ‘Jˆعگ}‚ًچى‚邾‚¯‚إ‚à”ٌڈي‚ة–ت“|‚إ‚·پB
ˆمٹw•”‚ج–â‘è‚ب‚ج‚إ‚·‚ھپAڈo‘èژز‚حˆمژtژu–]ژز‚ةپAژèٹش‚ج‚©‚©‚éچى‹ئ‚ًگ³ٹm‚©‚آŒّ—¦“I‚ةڈˆ—‚·‚é”\—ح‚ً‹پ‚ك‚ؤ‚¢‚é‹C‚ھ‚µ‚ـ‚·پB
چs—ٌ‚ً—p‚¢‚ؤ‰ً“ڑ‚³‚¹‚é(چs—ٌ‚جگد‚ًژQڈئ)‚و‚¤‚ة‚ب‚ء‚ؤ‚¢‚ـ‚·‚ھپA‰ً“ڑ‚جŒ`ژ®‚ھچs—ٌ‚ة‚ب‚ء‚ؤ‚¢‚éپA‚ئ‚¢‚¤‚¾‚¯‚إپAچs—ٌ‚ج–â‘è‚ئ‚µ‚ؤ‚ج—v‘f‚ح‚ ‚è‚ـ‚¹‚ٌپB
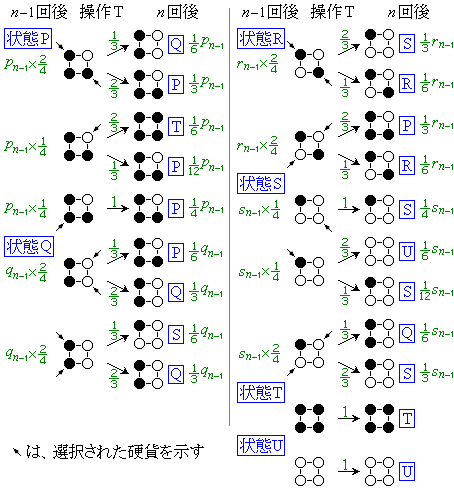
ˆب‰؛‚إ‚حپA•\‚ًڈم‚ة‚µ‚½چd‰ف‚ھپA‚؟‚ه‚¤‚ا1–‡‚¾‚¯‚ ‚éڈَ‘ش‚ًپuڈَ‘شPپvپA‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ•س‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éڈَ‘ش‚ًپuڈَ‘شQپvپA‚؟‚ه‚¤‚ا2–‡‚¾‚¯‚ ‚è‚»‚ê‚ç‚ھ‘خٹpگü‚ة‰ˆ‚ء‚ؤ•ہ‚ٌ‚إ‚¢‚éڈَ‘ش‚ًپuڈَ‘شRپvپA‚؟‚ه‚¤‚ا3–‡‚¾‚¯‚ ‚éڈَ‘ش‚ًپuڈَ‘شSپvپA4–‡‚ئ‚à— ‚ًڈم‚ة‚µ‚½ڈَ‘ش‚ًپuڈَ‘شTپvپA4–‡‚ئ‚à•\‚ًڈم‚ة‚µ‚½ڈَ‘ش‚ًپuڈَ‘شUپv‚ئ‚µ‚ـ‚·پB
ˆµ‚¤ڈَ‘ش‚ھ–â‘蕶‚ةڈo‚ؤ‚‚éڈَ‘شˆبٹO‚ة‚à‚ ‚è(ڈَ‘شTپCڈَ‘شU)پA•K‚¸‚µ‚àپA
‚ئ‚ب‚ç‚ب‚¢‚ج‚إپA’چˆس‚ھ•K—v‚إ‚·پB
 (1) ‘€چىT‚ًچs‚ء‚ؤپAڈ‰ٹْڈَ‘ش(ڈَ‘شQ‚إ‚·)‚©‚ç
(1) ‘€چىT‚ًچs‚ء‚ؤپAڈ‰ٹْڈَ‘ش(ڈَ‘شQ‚إ‚·)‚©‚ç پC
پC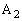 پC
پC پC
پC ‚ً‘I‘ً‚µ‚½‚ئ‚«‚جڈَ‹µ‚ًژ¦‚µ‚½‚à‚ج‚ھ‰Eگ}‚إ‚·پB‚ب‚¨پAپ›‚ھ•\‚ًڈم‚ة‚µ‚½چd‰فپAپœ‚ھ— ‚ًڈم‚ة‚µ‚½چd‰ف‚ً•\‚µ‚ـ‚·پB
‚ً‘I‘ً‚µ‚½‚ئ‚«‚جڈَ‹µ‚ًژ¦‚µ‚½‚à‚ج‚ھ‰Eگ}‚إ‚·پB‚ب‚¨پAپ›‚ھ•\‚ًڈم‚ة‚µ‚½چd‰فپAپœ‚ھ— ‚ًڈم‚ة‚µ‚½چd‰ف‚ً•\‚µ‚ـ‚·پB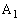 ‚ً‘I‘ً‚·‚é‚ئ
‚ً‘I‘ً‚·‚é‚ئ ‚ئ‚ب‚é‚ج‚إپA
‚ئ‚ب‚é‚ج‚إپA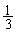 ‚جٹm—¦‚إ‡@‚جڈَ‘شP‚ةˆعچs‚µپA
‚جٹm—¦‚إ‡@‚جڈَ‘شP‚ةˆعچs‚µپA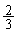 ‚جٹm—¦‚إ‡A‚جڈَ‘شQ‚ج‚ـ‚ـ‚ة‚ب‚è‚ـ‚·پB
‚جٹm—¦‚إ‡A‚جڈَ‘شQ‚ج‚ـ‚ـ‚ة‚ب‚è‚ـ‚·پB
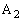 پC
پC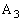 پC
پC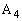 ‚ة‚آ‚¢‚ؤ‚àپA“¯—l‚ة‚µ‚ؤچl‚¦‚½‚ج‚ھ‰Eگ}‚إ‚·پB
‚ة‚آ‚¢‚ؤ‚àپA“¯—l‚ة‚µ‚ؤچl‚¦‚½‚ج‚ھ‰Eگ}‚إ‚·پB(‚ ) ‰Eگ}‚إپA‘€چىT‚ً1‰ٌچs‚ء‚½Œم‚ةڈَ‘شP‚ة‚ب‚é‚ج‚حپA‡@‚ئ‡B‚جڈêچ‡‚إپA‚±‚جٹm—¦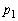 ‚حپA
‚حپA  ......[“ڑ]
......[“ڑ](‚¢) ‰Eگ}‚إپA‘€چىT‚ً1‰ٌچs‚ء‚½Œم‚ةڈَ‘شQ‚ة‚ب‚é‚ج‚حپA‡AپC‡CپC‡EپC‡G‚جڈêچ‡‚إپA‚±‚جٹm—¦ ‚حپA
‚حپA 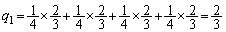 ......[“ڑ]
......[“ڑ](‚¤) ‰Eگ}‚إپA‘€چىT‚ً1‰ٌچs‚ء‚½Œم‚ةڈَ‘شR‚ة‚ب‚éڈêچ‡‚ح‚ب‚پA‚±‚جٹm—¦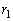 ‚حپA
‚حپA  ......[“ڑ]
......[“ڑ](‚¦) ‰Eگ}‚إپA‘€چىT‚ً1‰ٌچs‚ء‚½Œم‚ةڈَ‘شS‚ة‚ب‚é‚ج‚حپA‡D‚ئ‡F‚جڈêچ‡‚إپA‚±‚جٹm—¦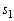 ‚حپA
‚حپA  ......[“ڑ]
......[“ڑ]
 (2) ‘€چىT‚ً
(2) ‘€چىT‚ً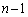 ‰ٌچs‚ء‚½ڈَ‘ش‚©‚çپAn‰ٌ–ع‚ج‘€چىT‚ًچs‚ء‚½‚ئ‚«‚جڈَ‹µ‚ً‰Eگ}‚ةژ¦‚µ‚ـ‚·پB
‰ٌچs‚ء‚½ڈَ‘ش‚©‚çپAn‰ٌ–ع‚ج‘€چىT‚ًچs‚ء‚½‚ئ‚«‚جڈَ‹µ‚ً‰Eگ}‚ةژ¦‚µ‚ـ‚·پB–îˆَ‚إ‘I‘ً‚³‚ꂽچd‰ف‚ًژ¦‚µ‚ـ‚·‚ھپA1‚آ‚جڈَ‘ش‚إ2‚آ‚ج–îˆَ‚ھ‚آ‚¢‚ؤ‚¢‚é‚ج‚حپA‚ا‚؟‚ç‚ج’¸“_‚ً‘I‘ً‚µ‚ؤ‚à“¯‚¶ٹm—¦‚إ“¯‚¶ڈَ‘ش(چd‰ف‚ج•\— ‚جˆت’u‚ةˆل‚¢‚ح‚ ‚è‚ـ‚·‚ھ)‚ةژٹ‚邱‚ئ‚ًˆس–،‚µ‚ـ‚·پB
‘€چىT‚ً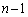 ‰ٌچs‚ء‚½ڈَ‘ش‚ة‚حپAڈَ‘شPپ`ڈَ‘شU‚ج6’ت‚è‚جڈَ‘ش‚ھ‚ ‚èپAڈَ‘شPپCڈَ‘شQپCڈَ‘شRپCڈَ‘شS‚ئ‚ب‚éٹm—¦‚ح
‰ٌچs‚ء‚½ڈَ‘ش‚ة‚حپAڈَ‘شPپ`ڈَ‘شU‚ج6’ت‚è‚جڈَ‘ش‚ھ‚ ‚èپAڈَ‘شPپCڈَ‘شQپCڈَ‘شRپCڈَ‘شS‚ئ‚ب‚éٹm—¦‚ح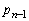 پC
پC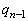 پC
پC پC
پC ‚إ‚·پB
‚إ‚·پB
‰Eگ}‚إ‚حپA‘€چىT‚ً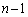 ‰ٌچs‚ء‚½ŒمپA—ل‚¦‚خپAڈَ‘شP‚ة‚¨‚¢‚ؤپAٹm—¦
‰ٌچs‚ء‚½ŒمپA—ل‚¦‚خپAڈَ‘شP‚ة‚¨‚¢‚ؤپAٹm—¦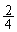 ‚إ
‚إ ‚©
‚©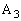 ‚ھ‘I‘ً‚³‚ê‚ؤ
‚ھ‘I‘ً‚³‚ê‚ؤ ‚ئ‚ب‚èپAٹm—¦
‚ئ‚ب‚èپAٹm—¦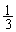 ‚إڈَ‘شQ‚ةˆعچs‚µپAٹm—¦
‚إڈَ‘شQ‚ةˆعچs‚µپAٹm—¦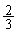 ‚إڈَ‘شP‚ج‚ـ‚ـ‚ئ‚ب‚è‚ـ‚·پBٹm—¦
‚إڈَ‘شP‚ج‚ـ‚ـ‚ئ‚ب‚è‚ـ‚·پBٹm—¦ ‚إ
‚إ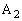 ‚ھ‘I‘ً‚³‚ê‚ؤ
‚ھ‘I‘ً‚³‚ê‚ؤ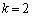 ‚ئ‚ب‚èپAٹm—¦
‚ئ‚ب‚èپAٹm—¦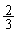 ‚إڈَ‘شT‚ةˆعچs‚µپAٹm—¦
‚إڈَ‘شT‚ةˆعچs‚µپAٹm—¦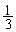 ‚إڈَ‘شP‚ج‚ـ‚ـ‚ئ‚ب‚è‚ـ‚·پB‚ـ‚½پAٹm—¦
‚إڈَ‘شP‚ج‚ـ‚ـ‚ئ‚ب‚è‚ـ‚·پB‚ـ‚½پAٹm—¦ ‚إ
‚إ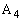 ‚ھ‘I‘ً‚³‚ê‚ؤ
‚ھ‘I‘ً‚³‚ê‚ؤ ‚ئ‚ب‚èپA•K‚¸ڈَ‘شP‚ج‚ـ‚ـ‚ة‚ب‚è‚ـ‚·پB
‚ئ‚ب‚èپA•K‚¸ڈَ‘شP‚ج‚ـ‚ـ‚ة‚ب‚è‚ـ‚·پB
‘€چىT‚ً ‰ٌچs‚ء‚½ŒمپAڈَ‘شQپCڈَ‘شRپCڈَ‘شS‚ة‚ ‚éڈêچ‡‚à“¯—l‚ة‚µ‚ؤچl‚¦‚½‚ج‚ھ‰Eگ}‚إ‚·پBڈَ‘شTپCڈَ‘شU‚ة‚ ‚éڈêچ‡‚ة‚حپA•K‚¸پAn‰ٌ‘€چىŒم‚àڈَ‘شTپCڈَ‘شU‚ج‚ـ‚ـ‚ة‚ب‚è‚ـ‚·پB
‰ٌچs‚ء‚½ŒمپAڈَ‘شQپCڈَ‘شRپCڈَ‘شS‚ة‚ ‚éڈêچ‡‚à“¯—l‚ة‚µ‚ؤچl‚¦‚½‚ج‚ھ‰Eگ}‚إ‚·پBڈَ‘شTپCڈَ‘شU‚ة‚ ‚éڈêچ‡‚ة‚حپA•K‚¸پAn‰ٌ‘€چىŒم‚àڈَ‘شTپCڈَ‘شU‚ج‚ـ‚ـ‚ة‚ب‚è‚ـ‚·پB
‰Eگ}‚و‚èپA‘€چىT‚ًn‰ٌچs‚ء‚½ŒمپAڈَ‘شPپCڈَ‘شQپCڈَ‘شRپCڈَ‘شS‚ئ‚ب‚éٹm—¦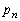 پC
پC پC
پC پC
پC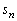 ‚حپA
‚حپA پC
پC پC
پC پC
پC ‚ئڈ‘‚©‚ê‚ؤ‚¢‚éڈَ‘ش‚جٹm—¦‚ً‰ء‚¦چ‡‚ي‚¹‚邱‚ئ‚ة‚و‚èپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
‚ئڈ‘‚©‚ê‚ؤ‚¢‚éڈَ‘ش‚جٹm—¦‚ً‰ء‚¦چ‡‚ي‚¹‚邱‚ئ‚ة‚و‚èپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB  پ@¥¥¥‡@
پ@¥¥¥‡@
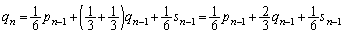 پ@¥¥¥‡A
پ@¥¥¥‡A
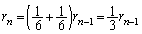 پ@¥¥¥‡B
پ@¥¥¥‡B
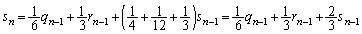 پ@¥¥¥‡C
پ@¥¥¥‡Cˆبڈم‚و‚èپA(‚¨) 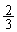 پ@(‚©)
پ@(‚©) 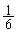 پ@(‚«)
پ@(‚«)  پ@(‚)
پ@(‚) 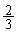 پ@(‚¯) 0پ@(‚±) 0پ@(‚³)
پ@(‚¯) 0پ@(‚±) 0پ@(‚³) 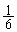 پ@(‚µ)
پ@(‚µ) 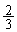 ......[“ڑ]
......[“ڑ] (‚·) (‚¤)‚جŒ‹‰ت‚ئ‡B‚و‚èپA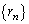 ‚حڈ‰چ€0پCŒِ”ن
‚حڈ‰چ€0پCŒِ”ن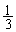 ‚ج“™”نگ”—ٌ‚إپA
‚ج“™”نگ”—ٌ‚إپA 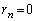 ......[“ڑ]
......[“ڑ]
(3) (‚·)‚جŒ‹‰ت‚ئ‡@‚و‚èپA
 پ@¥¥¥‡D
پ@¥¥¥‡D(‚·)‚جŒ‹‰ت‚ئ‡C‚و‚èپA
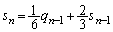 پ@¥¥¥‡E
پ@¥¥¥‡E‡Dپ|‡E‚و‚èپA
‚±‚ê‚ئپA(‚ )‚ئ(‚¦)‚جŒ‹‰ت‚و‚èپA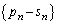 ‚حڈ‰چ€
‚حڈ‰چ€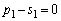 پCŒِ”ن
پCŒِ”ن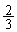 ‚ج“™”نگ”—ٌ‚إپA
‚ج“™”نگ”—ٌ‚إپA ‚ن‚¦‚ةپA”Cˆس‚جn‚ة‘خ‚µ‚ؤپA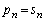
(4) (3)‚جŒ‹‰تپA‹y‚ر‡A‚و‚èپA
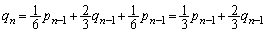 پ@¥¥¥‡F
پ@¥¥¥‡F‡Dپ~ پ{‡F‚و‚èپA
پ{‡F‚و‚èپA ‚±‚ê‚ئپA(‚ )(‚¢)‚جŒ‹‰ت‚و‚èپA ‚حپAڈ‰چ€
‚حپAڈ‰چ€ پCŒِ”ن
پCŒِ”ن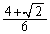 ‚ج“™”نگ”—ٌپB
‚ج“™”نگ”—ٌپB
پˆ 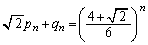 پ@¥¥¥‡G(‚¹)
پ@¥¥¥‡G(‚¹) 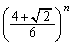 ......[“ڑ]‡Dپ~
......[“ڑ]‡Dپ~ پ{‡F‚و‚èپA
پ{‡F‚و‚èپA ‚±‚ê‚ئپA(‚ )(‚¢)‚جŒ‹‰ت‚و‚èپA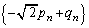 ‚حپAڈ‰چ€
‚حپAڈ‰چ€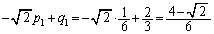 پCŒِ”ن
پCŒِ”ن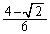 ‚ج“™”نگ”—ٌپB
‚ج“™”نگ”—ٌپB
پˆ  پ@¥¥¥‡H(‚»)
پ@¥¥¥‡H(‚») 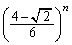 ......[“ڑ]
......[“ڑ]
(‡Gپ|‡H)پ€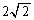 ‚و‚èپA
‚و‚èپA (‡Gپ{‡H)پ€2‚و‚èپA
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
پ@پ@گ”ٹwTOPپ@پ@TOPƒyپ[ƒW‚ة–ك‚é
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
‹êٹwٹyٹwڈm گڈژ“ü‰ïژَ•t’†پI—Œn‘هٹwژَŒ±ƒlƒbƒgڈm‹êٹwٹyٹwڈm(‚²ˆؤ“à‚ح‚±‚؟‚ç)‚²“ü‰ï‚حپA
‚ـ‚¸پA‚±‚؟‚ç‚ـ‚إƒپپ[ƒ‹‚ً
‚¨‘—‚è‚‚¾‚³‚¢پB