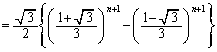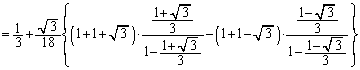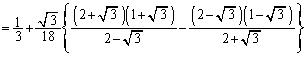�c�嗝�H���w'09�N[A2]
��������𓊂���Ƃ������s���J��Ԃ��s���B�������A2��A������5�ȏ�̖ڂ��o���ꍇ�́A����ȍ~�̎��s�͍s��Ȃ����̂Ƃ���B
n��ڂ̎��s���s���A����n��ڂɏo���ڂ�4�ȉ��ɂȂ�m����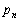 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A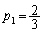 �C
�C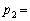 �@�P�@�C
�@�P�@�C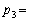 �@�R�@�ł���B�܂�
�@�R�@�ł���B�܂�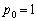 �Ƃ����B
�Ƃ����B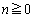 �ɑ��āA
�ɑ��āA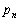 �C
�C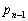 �C
�C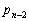 �̊Ԃɐ�������W�������߁A�����
�̊Ԃɐ�������W�������߁A�����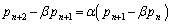 (
(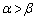 )�̌`�ɏ�����
)�̌`�ɏ�����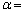 �@�T�@�ł���B����āA
�@�T�@�ł���B����āA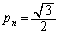 (�@�V�@)�ƂȂ�B
(�@�V�@)�ƂȂ�B
�܂��An��ڂ̎��s���s���A����n��ڂɏo���ڂ�5�ȏ�ɂȂ�m����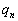 �Ƃ���B���̂Ƃ�
�Ƃ���B���̂Ƃ�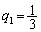 �ł���B
�ł���B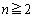 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A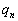 ��
��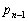 �C
�C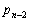 �̊Ԃɂ�
�̊Ԃɂ�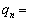 �@�X�@�Ȃ�W�������藧�B���������āA5�ȏ�̖ڂ��o��̊��Ғl��
�@�X�@�Ȃ�W�������藧�B���������āA5�ȏ�̖ڂ��o��̊��Ғl��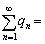 �@�Z�@�ł���B
�@�Z�@�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�܂��́A3���ԑQ���������Ă��邩�A�Ƃ����Ƃ��낪�����̕�����ڂɂȂ�܂��B���Ғl�ɂ��ẮA������������Ă��܂��Ă���̂ŁA���̒ʂ�Ɍv�Z����悢�̂ł����A���Ȃ�v�Z���ʓ|�Ȃ̂ŁA�~�X�ɂ͏[���ɒ��ӂ��Ă��������B
��������𓊂��āA5�ȏ�̖ڂ��o�鎖�ۂ�U (�m��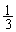 )�C4�ȉ��̖ڂ��o�鎖�ۂ�D (�m��
)�C4�ȉ��̖ڂ��o�鎖�ۂ�D (�m��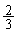 )�Ƃ��܂��B
)�Ƃ��܂��B
(�P) �K��2��ȏコ������𓊂���̂ŁA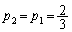 ......[��]
......[��] (�R) 3��߂�D���N����̂́A
�E1��ڂ�D��2��ڂ�U��3��ڂ�D�ɂȂ�(�m��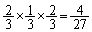 )�ꍇ�ƁA
)�ꍇ�ƁA �E2��ڂ�D��3��ڂ�U�ɂȂ�(�m��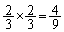 )�ꍇ
)�ꍇ ������A���҂��r���Ȃ̂ŁA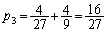 ......[��]
......[��] (�T) 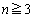 �̂Ƃ��An��ڂ�D���N����̂́A
�̂Ƃ��An��ڂ�D���N����̂́A �E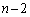 ��ڂ�D��
��ڂ�D��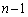 ��ڂ�U��n��ڂ�D�ɂȂ�(�m��
��ڂ�U��n��ڂ�D�ɂȂ�(�m��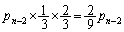 )�ꍇ�ƁA
)�ꍇ�ƁA �E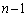 ��ڂ�D��n��ڂ�D�ɂȂ�(�m��
��ڂ�D��n��ڂ�D�ɂȂ�(�m��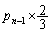 )�ꍇ
)�ꍇ ������A���҂͔r���Ȃ̂ŁA
����́A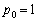 �Ȃ̂�
�Ȃ̂�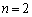 �̂Ƃ��ɂ����藧���܂��B
�̂Ƃ��ɂ����藧���܂��B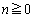 �Ƃ��āA
�Ƃ��āA �Ƃ���ƁA
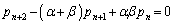 �@����B
�@����B(�V) �A���A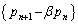 �́A�����F
�́A�����F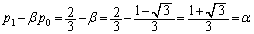 �C����α�����䐔���B����āA
�C����α�����䐔���B����āA 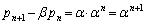 �@����C
�@����C�A��α�Cβ�����ւ��āA
������A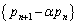 �́A�����F
�́A�����F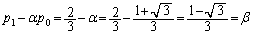 �C����β�̓��䐔��B����āA
�C����β�̓��䐔��B����āA 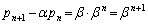 �@����D
�@����D�C�|�D���A
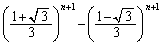 ......[��]
......[��](�X) 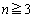 �̂Ƃ��An��ڂ�U���N����̂́A
�̂Ƃ��An��ڂ�U���N����̂́A �E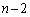 ��ڂ�D��
��ڂ�D��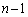 ��ڂ�U��n��ڂ�U�ɂȂ�(�m��
��ڂ�U��n��ڂ�U�ɂȂ�(�m��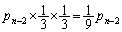 )�ꍇ�ƁA
)�ꍇ�ƁA �E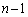 ��ڂ�D��n��ڂ�U�ɂȂ�(�m��
��ڂ�D��n��ڂ�U�ɂȂ�(�m��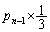 )�ꍇ
)�ꍇ ������A���҂͔r���Ȃ̂ŁA
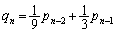 �@����E
�@����E�K��2��ȏコ������𓊂���̂�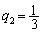 �ł�(
�ł�(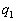 ��
��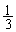 )���A
)���A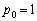 ���A
���A ���A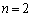 �̂Ƃ����E�͐������܂��B
�̂Ƃ����E�͐������܂��B 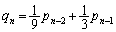 ......[��]
......[��](�Z) 5�ȏ�̖ڂ��o������Ғl�́A 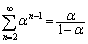 �C
�C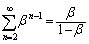
�� 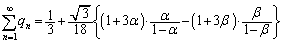
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B