慶大理工数学'09年[A3]
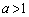 とする。xy平面上において点
とする。xy平面上において点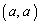 を中心とする半径rの円
を中心とする半径rの円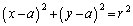 を考える。この円が曲線C:
を考える。この円が曲線C: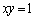 (
(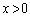 )に接するのは、半径rがどのような値のときであるかを調べてみよう。この半径rの円が曲線Cと接するとき、その接点のx座標は、曲線
)に接するのは、半径rがどのような値のときであるかを調べてみよう。この半径rの円が曲線Cと接するとき、その接点のx座標は、曲線
と直線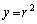 が接する場合の接点のx座標と一致する。
が接する場合の接点のx座標と一致する。
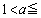 ソ のとき、
ソ のとき、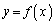 は
は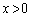 において
において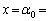 タ でのみ極小となる。よって、x座標が
タ でのみ極小となる。よって、x座標が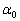 なる点において半径
なる点において半径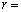 チ の円だけが曲線Cに接する。
チ の円だけが曲線Cに接する。
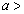 ソ のとき、
ソ のとき、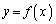 は
は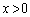 において
において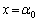 で極大となり、
で極大となり、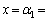 ツ ,
ツ ,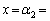 テ (
テ (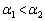 )において極小となる。したがって、x座標が
)において極小となる。したがって、x座標が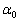 なる点で曲線Cに接する円のほかに、半径
なる点で曲線Cに接する円のほかに、半径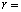 ト の円がx座標が
ト の円がx座標が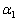 ,
,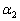 なる2点において曲線Cに接する。
なる2点において曲線Cに接する。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円と直角双曲線が複雑にからまりながら微妙な接し方をする、という問題です。誘導の仕方がちょっと変わっているので、まごつくかも知れませんが、出題者の意図をよく考えるようにしましょう。
なお、微分法の方程式への応用2を参照してください。
方程式: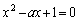 は、判別式:
は、判別式: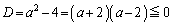 のとき実数解を持たないか重解をもち、このとき、
のとき実数解を持たないか重解をもち、このとき、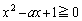 (2次方程式の一般論を参照)です。
(2次方程式の一般論を参照)です。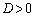 の場合には,
の場合には,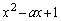 は正負いずれの値も取り得ます。
は正負いずれの値も取り得ます。
そこで、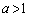 においては、
においては、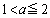 ,
,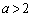 で場合分けします。
で場合分けします。 2 ......[答]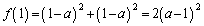
(タ) 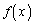 は
は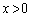 において
において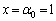 ......[答] でのみ極小となります。
......[答] でのみ極小となります。 (チ) 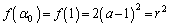
より、半径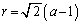 ......[答] の円だけが曲線Cに接します。
......[答] の円だけが曲線Cに接します。 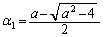 ,
,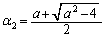
ここで、
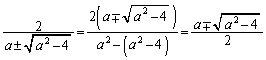 (複号同順)
(複号同順)より、
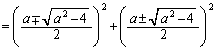 (ここまで複号同順)
(ここまで複号同順)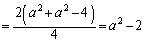
(ツ) 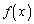 は
は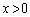 において
において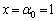 で極大となり、
で極大となり、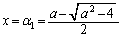 ......[答],
......[答], (テ) 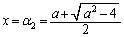 ......[答]において極小となります。
......[答]において極小となります。 (ト) したがって、x座標が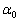 (
(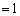 )なる点で曲線Cに接する円のほかに、半径
)なる点で曲線Cに接する円のほかに、半径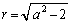 ......[答] の円がx座標が
......[答] の円がx座標が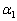 ,
, なる2点において曲線Cに接することになります。
なる2点において曲線Cに接することになります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 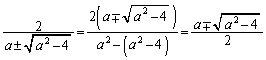 (複号同順)
(複号同順)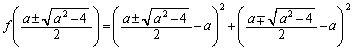
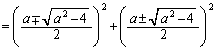 (ここまで複号同順)
(ここまで複号同順)