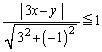慶大理工数学'10年[A3]
座標平面上において、以下の設問(1),(2),(3)のように図形Sと点Pを考える。図形S上を点Qが動くとき、線分PQの長さの最小値を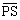 と表す。
と表す。
(1) 方程式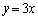 の表す図形をSとする。点P
の表す図形をSとする。点P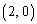 について
について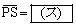 である。また、
である。また、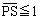 を満たす点P
を満たす点P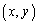 全体が描く図形は、不等式
全体が描く図形は、不等式 の表す領域と一致する。
(2) 方程式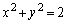 の表す図形をSとする。点P
の表す図形をSとする。点P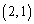 について
について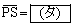 である。また、
である。また、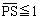 を満たす点P
を満たす点P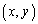 全体が描く図形の面積は
全体が描く図形の面積は である。
である。 (3) 2つの式
の表す図形をSとする。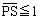 を満たす点P
を満たす点P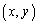 全体が描く図形を図示しなさい。
全体が描く図形を図示しなさい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 論述式であれば、どう論述するか悩む点があるかも知れませんが、空所を補充して図形を図示するだけなので、わざわざ面倒なことを考える必要はないでしょう。
(1)(ス) 点Pと直線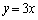 上を動く点Qとの距離の最小値は、点Pと直線
上を動く点Qとの距離の最小値は、点Pと直線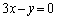 との距離にほかなりません。点と直線の距離の公式より、
との距離にほかなりません。点と直線の距離の公式より、 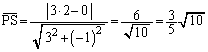 ......[答]
......[答](セ)(ソ) 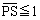 を満たす点P
を満たす点P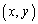 は、直線
は、直線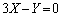 との距離が1以下となる点で、
との距離が1以下となる点で、 ∴ 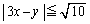 絶対値を外すと、
絶対値を外すと、 ∴ 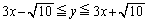
(セ) 3 (ソ) 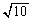 ......[答]
......[答]
(2)(タ) 点Pと円周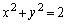 上を動く点Qとの距離の最小値は、点Pと円周の中心
上を動く点Qとの距離の最小値は、点Pと円周の中心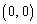 との距離から円周の半径を引いたものに等しく、
との距離から円周の半径を引いたものに等しく、 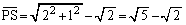 ......[答]
......[答](チ) 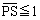 を満たす点P
を満たす点P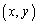 は、円周
は、円周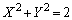 上の点から距離1以下の点ですが、点Pが描く図形は、原点を中心とする半径
上の点から距離1以下の点ですが、点Pが描く図形は、原点を中心とする半径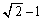 の円周から外側であって、かつ、原点を中心とする半径
の円周から外側であって、かつ、原点を中心とする半径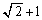 の円周から内側となる図形で、その面積は、
の円周から内側となる図形で、その面積は、 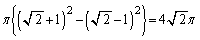 ......[答]
......[答]
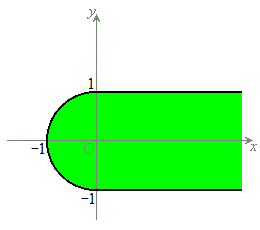 (3) 図形Sはx軸の原点から右の部分です。
(3) 図形Sはx軸の原点から右の部分です。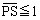 を満たすのは、
を満たすのは、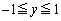 かつ
かつ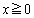 となる部分、または、原点を中心とする半径1の円の内側となる点で、図示すると右図黄緑色着色部(境界線を含む)。
となる部分、または、原点を中心とする半径1の円の内側となる点で、図示すると右図黄緑色着色部(境界線を含む)。
追記.論述する場合には、媒介変数表示を利用するのがよいでしょう。
(1) 点P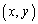 について、直線
について、直線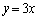 上の点をQ
上の点をQ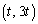 (tは実数)として、線分PQの長さは、
(tは実数)として、線分PQの長さは、 (2) 点P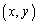 について、円周
について、円周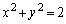 上の点をQ
上の点をQ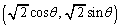 (
(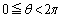 )として、線分PQの長さは、
)として、線分PQの長さは、 より、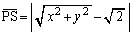 (原点とPとの距離から半径を引いたもの)点Pが
(原点とPとの距離から半径を引いたもの)点Pが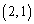 のとき、
のとき、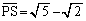
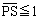 のとき、
のとき、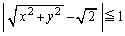 ∴
∴ 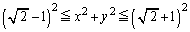
(3) S上の点はQ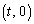 (
(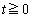 )と表せます。P
)と表せます。P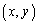 のとき、線分PQの長さは
のとき、線分PQの長さは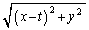 です。
です。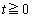 より、
より、 (ii) 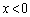 のとき、線分PQの長さは、
のとき、線分PQの長さは、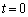 のときに最小値
のときに最小値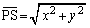
よって、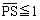 を満たすのは、
を満たすのは、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 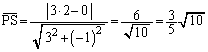 ......[答]
......[答]