�c�嗝�H���w'10�N[A4]
���̐���n�Ck�ɑ��āAx��3����
���l����B3��������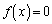 �����قȂ�3�̎����������悤�Ȑ��̐����̑g
�����قȂ�3�̎����������悤�Ȑ��̐����̑g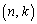 �����������B
�����������B
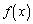 �̓�����
�̓�����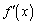 �Ƃ���B
�Ƃ���B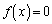 �����قȂ�3�̎����������Ȃ�A
�����قȂ�3�̎����������Ȃ�A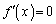 �̑��قȂ�������̌���
�̑��قȂ�������̌��� �łȂ���Ȃ�Ȃ��B������An��k�̖������s����
�łȂ���Ȃ�Ȃ��B������An��k�̖������s����
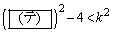 �@����@
�@����@
����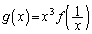 �Ƃ����ƁA
�Ƃ����ƁA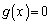 �����قȂ�3�̎������������Ȃ���Ȃ�Ȃ��B������A�@���̂Ɠ��l�ɂ��āAn��k�̖������s����
�����قȂ�3�̎������������Ȃ���Ȃ�Ȃ��B������A�@���̂Ɠ��l�ɂ��āAn��k�̖������s����
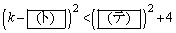 �@����A
�@����A
���̐���n��^����Ƃ��A�A���s�����@�C�A�������̐���k�����ׂċ��߂��
��3�ł���B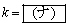 �ɑ��āA������
�ɑ��āA������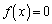 ���l����ƁA�����n�ɖ��W�ɒ�܂��
���l����ƁA�����n�ɖ��W�ɒ�܂��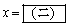 ��n��p���ĕ\�����2�̉�
��n��p���ĕ\�����2�̉�
��3�̎����������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�g�̌`���q���g�ɂȂ��Ă��܂��B�U���ɂ��܂�����ĉ�i�߂܂��傤�B
(�c) 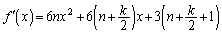
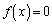 �����قȂ�3�̎����������Ȃ�A
�����قȂ�3�̎����������Ȃ�A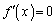 �̑��قȂ�������̌���2�łȂ���Ȃ�܂���(�����@�̕������ւ̉��p���Q��)�B2 ......[��]
�̑��قȂ�������̌���2�łȂ���Ȃ�܂���(�����@�̕������ւ̉��p���Q��)�B2 ......[��]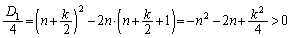
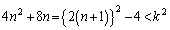 �@����@
�@����@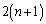 ......[��]
......[��](�g) 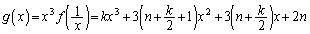
�@���̂Ɠ��l�ɂ��āA2��������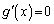 �̔��ʎ�
�̔��ʎ�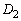 �ɂ��āA
�ɂ��āA 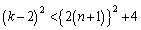 �@����A
�@����A2 ......[��]
(�i) �@�ɂ��āA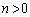 ���A
���A �� 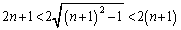 �@����B
�@����B
�A�ɂ��āA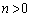 ���A
���A �� 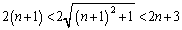 �@����C
�@����C
�@��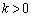 ���A
���A 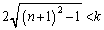 �@����D
�@����D�A��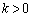 ���A
���A 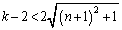 �@����E
�@����E�D�C�E���A
���̕s������������k�́A�B�C�C���l������ƁA
�����A
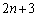 ......[��]
......[��](�j) 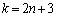 �̂Ƃ��A
�̂Ƃ��A 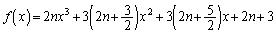 �@����F
�@����F�un�ɖ��W�ɒ�܂���v�Ƃ�����蕶�̋L�q����Ax��1�C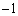 �C����Ə��ɑ�����čs���܂��B
�C����Ə��ɑ�����čs���܂��B 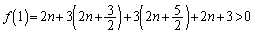
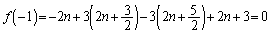 �@����G
�@����G������A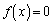 �͉�
�͉�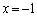 �������܂��B
�������܂��B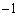 ......[��]
......[��] (�k) �G���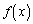 ��
��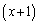 �������ɂ���(�����藝���Q��)�̂ŁA�F��
�������ɂ���(�����藝���Q��)�̂ŁA�F��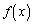 ��
��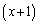 �Ŋ����āA
�Ŋ����āA (�l) 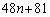 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B