慶大理工数学'11年[B1]
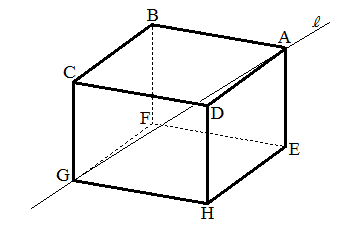 座標空間で次の8つの点
座標空間で次の8つの点
を頂点とする1辺の長さ2の立方体ABCD-EFGHを考える。いま、点P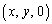 を正方形EFGH内の点(辺上も含む、ただし
を正方形EFGH内の点(辺上も含む、ただし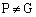 )とし、点Aと点Gを通る直線を
)とし、点Aと点Gを通る直線を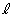 とする。
とする。
(1) 点Qを直線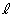 上の点で
上の点で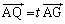 (t は実数)を満たすものとする。
(t は実数)を満たすものとする。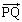 と
と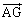 が直交するときt をxとyで表すと
が直交するときt をxとyで表すと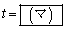 となる。
となる。 (2) 点Pから直線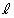 に下ろした垂線の足は点Aと点Gの間にあることを証明せよ。
に下ろした垂線の足は点Aと点Gの間にあることを証明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (3)では、図形的に見ていくことも可能ですが、素直に計算でやってみます。腕尽く計算だとかなり面倒になります。なお、空間ベクトルを参照してください。
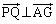 より、
より、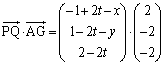
∴ 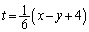
(マ) 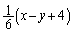 ......[答]
......[答]
(2) P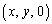 は正方形EFGH内の点であることから、
は正方形EFGH内の点であることから、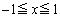 ,
,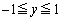
ただし、 より、
より、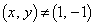
よって、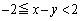 ,
,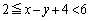
∴ 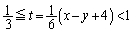
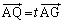 より、点Pから直線
より、点Pから直線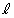 に下ろした垂線の足は点Aと点Gの間にあります。(証明終)
に下ろした垂線の足は点Aと点Gの間にあります。(証明終)
(3) PからAGに垂線PQを下ろすと、(1)で、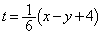 ,
,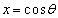 ,
,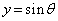 とすることにより、
とすることにより、 これより、
三角形APGの面積は、AGを底辺と見ると、高さPQが最大のとき最大、高さPQが最小のとき最小で、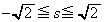 より、
より、
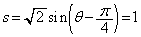 ,つまり、
,つまり、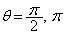 のとき、
のとき、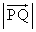 は最大値
は最大値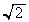 をとり、このとき、三角形APGの面積は最大値
をとり、このとき、三角形APGの面積は最大値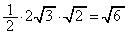 をとります。
をとります。
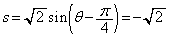 ,つまり、
,つまり、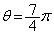 のとき、
のとき、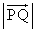 は最小値
は最小値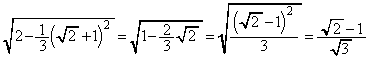 をとり、このとき、三角形APGの面積は最小値
をとり、このとき、三角形APGの面積は最小値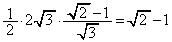 をとる。
をとる。
最大値: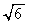 (
(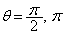 のとき),最小値:
のとき),最小値: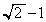 (
(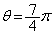 のとき) ......[答]
のとき) ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 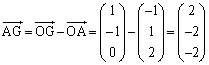
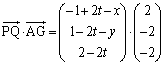
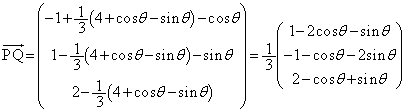
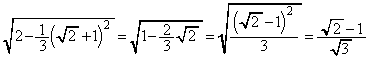 をとり、このとき、三角形APGの面積は最小値
をとり、このとき、三角形APGの面積は最小値