慶應大学理工学部2011年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[A1](1) 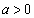 とする。定積分
とする。定積分 の値は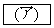 である。
である。 (2) kを実数とする。座標平面上で、点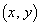 を直線
を直線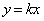 に関して対称移動した点を
に関して対称移動した点を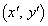 とすると
とすると が成り立つ。
(3) 負でない実数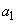 ,
,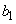 ,
,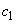 で
で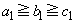 を満たすものが与えられているとき、数列
を満たすものが与えられているとき、数列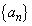 ,
,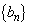 ,
,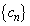 を次のように定める。
を次のように定める。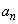 ,
,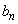 ,
,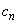 に対して
に対して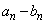 ,
,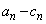 ,
,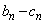 を大きさの順に並べ、大きい順に
を大きさの順に並べ、大きい順に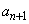 ,
,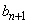 ,
,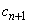 とする。たとえば
とする。たとえば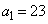 ,
,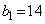 ,
,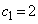 とするとき、
とするとき、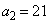 ,
,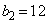 ,
,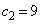 であり、
であり、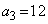 ,
,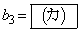 ,
,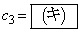 である。
である。 次に、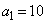 で
で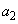 ,
,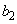 ,
,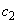 はどれも0ではなく
はどれも0ではなく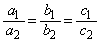 が満たされているとする。このとき
が満たされているとする。このとき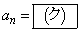 である。
である。 [解答へ]
[A2] kを実数として、xの4次関数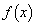 を
を
と定める。
(1)方程式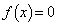 は、kの値によらず
は、kの値によらず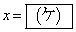 を実数解としてもつ。また、この方程式の実数解が
を実数解としてもつ。また、この方程式の実数解が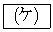 のみとなるのは、
のみとなるのは、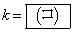 のときである。
のときである。 (3) 方程式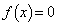 が相異なる4つの実数解をもつようなkの値の範囲は、
が相異なる4つの実数解をもつようなkの値の範囲は、 である。kがこの範囲にあるとき、
である。kがこの範囲にあるとき、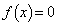 の4つの解をa,b,c,d (
の4つの解をa,b,c,d (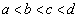 )とする。
)とする。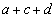 と
と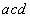 をそれぞれkを用いて表すと、
をそれぞれkを用いて表すと、 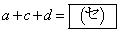 ,
,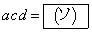
となる。また、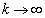 のとき、
のとき、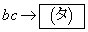 である。
である。 [解答へ]
[A3] 実数θ は
の範囲を動くとする。空間内の動点P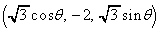 と点Q
と点Q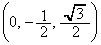 を通る直線が、xy平面と交わる点をR
を通る直線が、xy平面と交わる点をR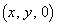 とする。x,yをθ の関数として表すと、
とする。x,yをθ の関数として表すと、
 ,
,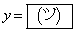
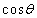 と
と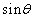 をx,yを用いて表すと、
をx,yを用いて表すと、
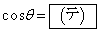 ,
,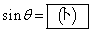
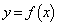 とすれば、
とすれば、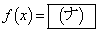 となる。
となる。
次に、xy平面内の領域Dを
と定め、領域Dの面積を求めることを考える。直線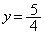 を原点O
を原点O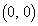 を中心として、
を中心として、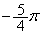 回転した直線の方程式は
回転した直線の方程式は となる。また、曲線
となる。また、曲線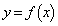 を原点を中心として、
を原点を中心として、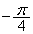 回転した曲線の方程式を
回転した曲線の方程式を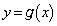 (
(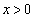 )とすれば、
)とすれば、
となる。領域Dを原点を中心として、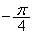 回転した領域を
回転した領域を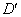 とすれば、領域Dと領域
とすれば、領域Dと領域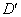 は合同だから、
は合同だから、
である。
[解答へ]
[A4] 1辺の長さが1の正五角形の5つの頂点に反時計回りにA,B,C,D,Eと名前をつける。いま、初めに頂点Aに白玉を1個、頂点Cに赤玉を1個置き次の操作を繰り返し行う。
| [操作] コイン1枚とさいころ1個を同時に投げる。コインの表が出たら白玉を、裏が出たら赤玉を選んでさいころの出た目の数の長さだけ正五角形の辺上を反時計回りに動かす。また、玉が到達した頂点に別の色の玉がある場合は、玉を動かす前にあった2つの玉の位置を入れ替えるものとする。 |
例えば1回目にコインの表とさいころの6の目が出たとすると白玉がA→B→C→D→E→A→Bと動き、白玉の位置が頂点Bとなる。続いて2回目にコインの裏とさいころの4の目が出たとすると赤玉がC→D→E→A→Bと動き、到達した頂点Bに白玉があるので、赤玉を頂点Bに置き、頂点Bにあった白玉を頂点Cに移す。
以下、2つの玉が正五角形の隣り合う2頂点にある状態を「状態(S)」と呼ぶことにする。
(1) 2回目の操作を終えたとき頂点Dと頂点Eに玉がある確率は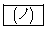 である。
である。 (2) n回目の操作を終えたとき状態(S)となる確率を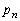 とする。
とする。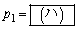 である。また
である。また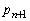 と
と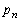 の間には
の間には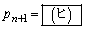 という関係式が成り立つ。これより
という関係式が成り立つ。これより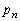 をnを用いて表すと
をnを用いて表すと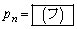 となる。
となる。 (3) n回目の操作を終えたとき初めて状態(S)となる確率を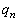 とする。
とする。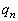 をnを用いて表すと
をnを用いて表すと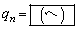 である。
である。 いま、状態(S)となるまで操作を繰り返し、状態(S)となった時点で操作を終了する。ただし、操作をr回行っても状態(S)とならない場合はr回で操作を終了することとする。このとき、操作を行う回数の期待値をrを用いて表すと となる。
となる。 [解答へ]
 [B1] 座標空間で次の8つの点
[B1] 座標空間で次の8つの点
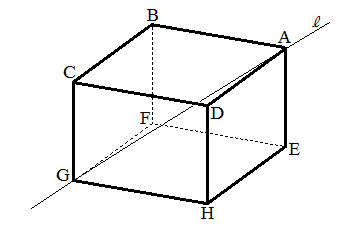
を頂点とする1辺の長さ2の立方体ABCD-EFGHを考える。いま、点P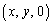 を正方形EFGH内の点(辺上も含む、ただし
を正方形EFGH内の点(辺上も含む、ただし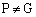 )とし、点Aと点Gを通る直線を
)とし、点Aと点Gを通る直線を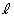 とする。
とする。
(1) 点Qを直線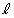 上の点で
上の点で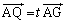 (t は実数)を満たすものとする。
(t は実数)を満たすものとする。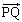 と
と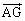 が直交するときt をxとyで表すと
が直交するときt をxとyで表すと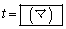 となる。
となる。 (2) 点Pから直線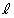 に下ろした垂線の足は点Aと点Gの間にあることを証明せよ。
に下ろした垂線の足は点Aと点Gの間にあることを証明せよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 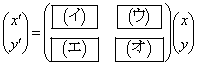
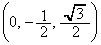 を通る直線が、xy平面と交わる点をR
を通る直線が、xy平面と交わる点をR