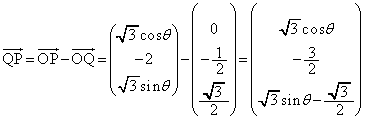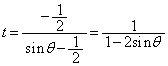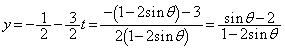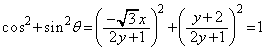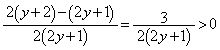�c�嗝�H���w'11�N[A3]
����θ ��
�͈̔͂��Ƃ���B��ԓ��̓��_P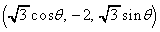 �Ɠ_Q
�Ɠ_Q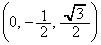 ��ʂ钼�����Axy���ʂƌ����_��R
��ʂ钼�����Axy���ʂƌ����_��R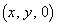 �Ƃ���Bx�Cy��θ �̊��Ƃ��ĕ\���ƁA
�Ƃ���Bx�Cy��θ �̊��Ƃ��ĕ\���ƁA
 �C
�C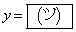
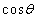 ��
��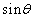 ��x�Cy��p���ĕ\���ƁA
��x�Cy��p���ĕ\���ƁA
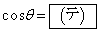 �C
�C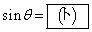
 �Ƃ���A
�Ƃ���A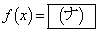 �ƂȂ�B
�ƂȂ�B
���ɁAxy���ʓ��̗̈�D��
�ƒ�߁A�̈�D�̖ʐς����߂邱�Ƃ��l����B���� �����_O
�����_O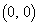 �𒆐S�Ƃ��āA
�𒆐S�Ƃ��āA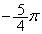 ��]���������̕�������
��]���������̕������� �ƂȂ�B�܂��A�Ȑ�
�ƂȂ�B�܂��A�Ȑ�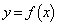 �����_�𒆐S�Ƃ��āA
�����_�𒆐S�Ƃ��āA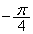 ��]�����Ȑ��̕�������
��]�����Ȑ��̕�������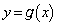 (
(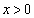 )�Ƃ���A
)�Ƃ���A
�ƂȂ�B�̈�D�����_�𒆐S�Ƃ��āA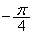 ��]�����̈��
��]�����̈��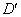 �Ƃ���A�̈�D�Ɨ̈�
�Ƃ���A�̈�D�Ɨ̈�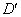 �͍���������A
�͍���������A
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�L���Ȑ������A�����ߖ��Ȃ̂ō��W��]�������o���܂ł��Ȃ��ł��傤�B
����PQ��̓_�́A
xy���ʏ�ł́A
�Ƃ��āA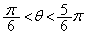 ���
���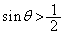 �Ȃ̂ŁA
�Ȃ̂ŁA
����āA
(�`) 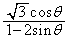 �@(�c)
�@(�c) 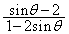 ......[��]
......[��]
(�e) 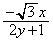 �@(�g)
�@(�g) 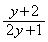 ......[��]
......[��]
�� 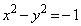 �@����A�@(�o�Ȑ����Q��)
�@����A�@(�o�Ȑ����Q��)
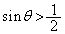 �Ƈ@���A
�Ƈ@���A
����āA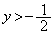
�A���A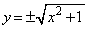 �ƂȂ�܂����A�����́A�|���Ƃ�ƁA
�ƂȂ�܂����A�����́A�|���Ƃ�ƁA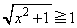 ���A
���A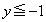 �ƂȂ��Ă��܂��̂ŁA�{���Ƃ邱�ƂɂȂ�܂��B����āA
�ƂȂ��Ă��܂��̂ŁA�{���Ƃ邱�ƂɂȂ�܂��B����āA
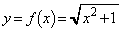 (
(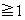 )
)
(�i) 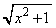 ......[��]
......[��]
����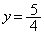 �ƌ��_�Ƃ̋�����
�ƌ��_�Ƃ̋�����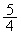 �ł��B����
�ł��B����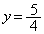 �����_O�𒆐S�Ƃ���
�����_O�𒆐S�Ƃ���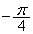 ��]�����Ƃ��X��
��]�����Ƃ��X��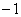 �̒����ɂȂ�܂����A���_�Ƃ̋����͂�͂�
�̒����ɂȂ�܂����A���_�Ƃ̋����͂�͂�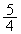 �ł��B�X��
�ł��B�X��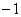 �̒�����
�̒�����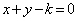 (
(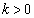 )�Ƃ��āA���_�Ƃ̋����́A
)�Ƃ��āA���_�Ƃ̋����́A
����āA��]��̒����̕������́A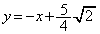 �@����B
�@����B
(�j) 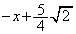 ......[��]
......[��]
�A��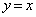 ��
��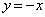 ��Q�ߐ��Ƃ��钼�p�o�Ȑ��ł��B�A��
��Q�ߐ��Ƃ��钼�p�o�Ȑ��ł��B�A��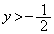 �̕�����
�̕�����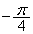 ��]����Ƒ�1�ی��ɗ��܂����A�Q�ߐ���x����y���ɂȂ�A���p�o�Ȑ���
��]����Ƒ�1�ی��ɗ��܂����A�Q�ߐ���x����y���ɂȂ�A���p�o�Ȑ���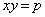 (p�F�萔)�ƂȂ�܂��B
(p�F�萔)�ƂȂ�܂��B
�A��y����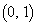 �Ō����܂����A���̓_��
�Ō����܂����A���̓_��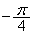 ��]�����
��]�����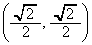 �ɗ��܂��B���p�o�Ȑ�
�ɗ��܂��B���p�o�Ȑ�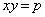 ��
��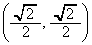 ��ʂ�̂ŁA
��ʂ�̂ŁA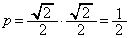
��]��̒��p�o�Ȑ���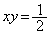 �C
�C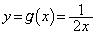 (��1�ی��ɂ���̂�
(��1�ی��ɂ���̂�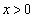 )�@����C
)�@����C
(�k) 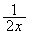 ......[��]
......[��]
�B�C�C��A������ƁA
�� 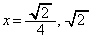
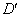 ���ʐ�S�́A
���ʐ�S�́A
(�l) 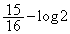 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B