�c�嗝�H���w'11�N[A1]
(1) 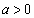 �Ƃ���B��ϕ�
�Ƃ���B��ϕ� �̒l��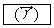 �ł���B
�ł���B (2) k�������Ƃ���B���W���ʏ�ŁA�_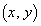 ��
��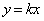 �Ɋւ��đΏ̈ړ������_��
�Ɋւ��đΏ̈ړ������_��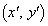 �Ƃ����
�Ƃ���� �����藧�B
(3) ���łȂ�����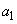 �C
�C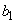 �C
�C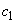 ��
��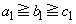 �������̂��^�����Ă���Ƃ��A����
�������̂��^�����Ă���Ƃ��A����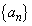 �C
�C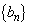 �C
�C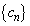 �����̂悤�ɒ�߂�B
�����̂悤�ɒ�߂�B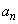 �C
�C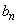 �C
�C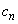 �ɑ���
�ɑ���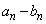 �C
�C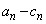 �C
�C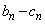 ��傫���̏��ɕ��ׁA�傫������
��傫���̏��ɕ��ׁA�傫������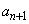 �C
�C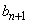 �C
�C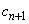 �Ƃ���B���Ƃ���
�Ƃ���B���Ƃ���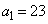 �C
�C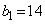 �C
�C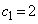 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A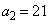 �C
�C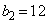 �C
�C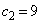 �ł���A
�ł���A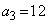 �C
�C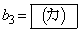 �C
�C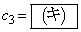 �ł���B
�ł���B ���ɁA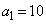 ��
��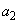 �C
�C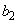 �C
�C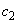 �͂ǂ��0�ł͂Ȃ�
�͂ǂ��0�ł͂Ȃ�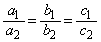 ����������Ă���Ƃ���B���̂Ƃ�
����������Ă���Ƃ���B���̂Ƃ�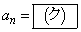 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�͂悭������ł����A(3)�͏����ʓ|�ł��B
(2)(i) 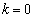 �̂Ƃ��A����
�̂Ƃ��A����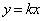 ��x���ł��B
��x���ł��B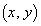 ��x���Ɋւ��đΏ̈ړ��������
��x���Ɋւ��đΏ̈ړ��������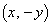 �ɗ��܂�(1���ϊ����Q��)�B����āA
�ɗ��܂�(1���ϊ����Q��)�B����āA 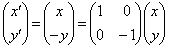 �@����@
�@����@(ii) 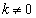 �̂Ƃ��A
�̂Ƃ��A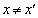 �ł��B
�ł��B �� 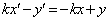 �@����A
�@����A
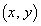 �C
�C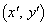 �����Ԓ����͒���
�����Ԓ����͒���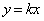 �ƒ�������̂ŁA�X���ɂ��āA
�ƒ�������̂ŁA�X���ɂ��āA �� 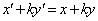 �@����B
�@����B
�A�C�B���s���p���ď����ƁA ������A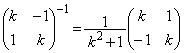 ��������(�t�s�����Q��)�ƁA
��������(�t�s�����Q��)�ƁA ���̌��ʂ͇@���܂�ł��܂��B(�C) 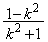 �@(�E)
�@(�E) 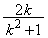 �@(�G)
�@(�G) 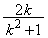 �@(�I)
�@(�I) 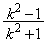 ......[��]
......[��]
(3) 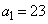 �C
�C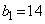 �C
�C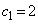 ���A
���A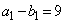 �C
�C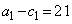 �C
�C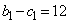 ��傫���̏��ɕ��ׂāA
��傫���̏��ɕ��ׂāA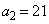 �C
�C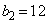 �C
�C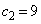
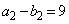 �C
�C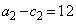 �C
�C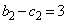 ��傫���̏��ɕ��ׂāA
��傫���̏��ɕ��ׂāA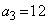 �C
�C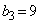 �C
�C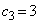 (�J) 9�@(�L) 3 ......[��]
(�J) 9�@(�L) 3 ......[��]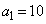 �C
�C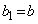 �C
�C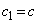 (
(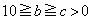 )�̂Ƃ��A
)�̂Ƃ��A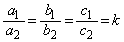 �Ƃ����ƁA
�Ƃ����ƁA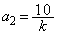 �C
�C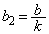 �C
�C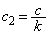 �C�܂��A
�C�܂��A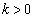 �ł��B
�ł��B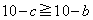 �ɒ��ӂ��āA�ȉ���3�ʂ�Ɍ����܂��B
�ɒ��ӂ��āA�ȉ���3�ʂ�Ɍ����܂��B(i) 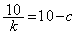 �C
�C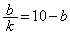 �C
�C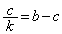 �̂Ƃ��A
�̂Ƃ��A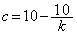 �C
�C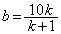 ���3���ɑ������ƁA
���3���ɑ������ƁA 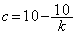 �C
�C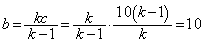
���3���ɑ������ƁA
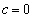 �ƂȂ��Ă��܂����߁A���̏ꍇ�͂��蓾�܂���B
�ƂȂ��Ă��܂����߁A���̏ꍇ�͂��蓾�܂���B(iii) 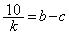 �C
�C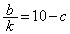 �C
�C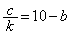 �̂Ƃ��A��1���Ƒ�2�����A
�̂Ƃ��A��1���Ƒ�2�����A 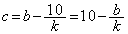 �C
�C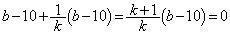
����āA(i)���A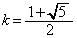
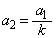 �C
�C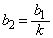 �C
�C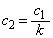 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A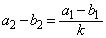 �C
�C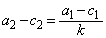 �C
�C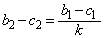 ���A
���A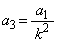 �C
�C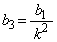 �C
�C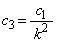 �C����C
�C����C (�N) 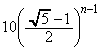 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 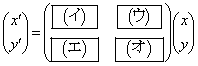
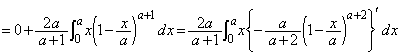
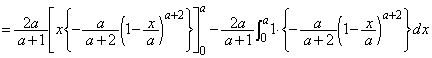
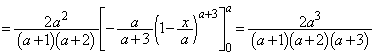 ......[��]
......[��]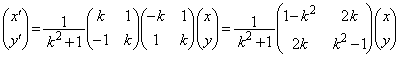
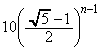 ......[��]
......[��]