�c�嗝�H���w'11�N[A2]
k�������Ƃ��āAx��4����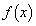 ��
��
�ƒ�߂�B
(1)������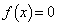 �́Ak�̒l�ɂ�炸
�́Ak�̒l�ɂ�炸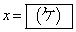 ���������Ƃ��Ă��B�܂��A���̕������̎�������
���������Ƃ��Ă��B�܂��A���̕������̎�������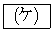 �݂̂ƂȂ�̂́A
�݂̂ƂȂ�̂́A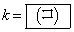 �̂Ƃ��ł���B
�̂Ƃ��ł���B (3) ������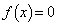 �����قȂ�4�̎����������悤��k�̒l�͈̔͂́A
�����قȂ�4�̎����������悤��k�̒l�͈̔͂́A �ł���Bk�����͈̔͂ɂ���Ƃ��A
�ł���Bk�����͈̔͂ɂ���Ƃ��A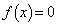 ��4�̉���a�Cb�Cc�Cd (
��4�̉���a�Cb�Cc�Cd (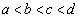 )�Ƃ���B
)�Ƃ���B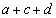 ��
��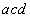 �����ꂼ��k��p���ĕ\���ƁA
�����ꂼ��k��p���ĕ\���ƁA 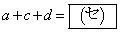 �C
�C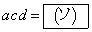
�ƂȂ�B�܂��A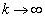 �̂Ƃ��A
�̂Ƃ��A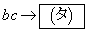 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@3�����A4�����A3���������A4���������Ɋւ�����e�L�x�Ȗ��ł��B
(1) 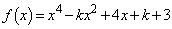
����āA������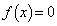 �́Ak�̒l�Ɋ�炸
�́Ak�̒l�Ɋ�炸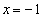 �����ɂ��B(�P)
�����ɂ��B(�P) 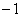 ......[��]
......[��]
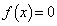 ��
�� 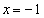 �܂���
�܂��� 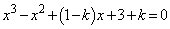
3���������F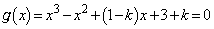 ���A
���A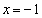 �����Ɏ����߂ɁA
�����Ɏ����߂ɁA �ł��邱�Ƃ��K�v�ŁA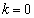
�t�ɁA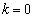 �̂Ƃ��A
�̂Ƃ��A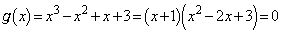 �́A
�́A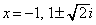 �����ɂ��̂ŁA
�����ɂ��̂ŁA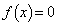 �̎�������
�̎�������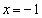 �݂̂ɂȂ�܂��B(�R) 0 ......[��]
�݂̂ɂȂ�܂��B(�R) 0 ......[��]
(2) 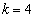 �̂Ƃ��A
�̂Ƃ��A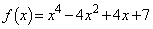
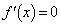 �Ƃ���ƁA
�Ƃ���ƁA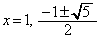
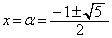 �Ƃ���ƁA
�Ƃ���ƁA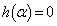 ���A
���A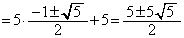 �@(��������)
�@(��������)�����\���A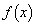 �́A
�́A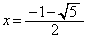 �ɂ����čŏ��l
�ɂ����čŏ��l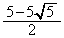 ���Ƃ�܂�(3�����̍ő�ŏ����Q��)�B(�T)
���Ƃ�܂�(3�����̍ő�ŏ����Q��)�B(�T) 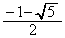 �@(�V)
�@(�V) 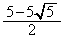 ......[��]
......[��]
(3) ������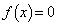 �����قȂ�4�̎����������Ƃ��A
�����قȂ�4�̎����������Ƃ��A ���A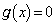 ��
��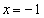 �ȊO�̑��قȂ�3�������������܂��B
�ȊO�̑��قȂ�3�������������܂��B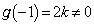 ���A
���A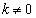 �@����@
�@����@ ���A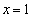 ��
��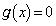 �̉��ɂȂ蓾�Ȃ��̂ŁA������
�̉��ɂȂ蓾�Ȃ��̂ŁA������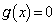 ���l�������ɁA
���l�������ɁA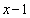 �Ŋ����āA
�Ŋ����āA ���l���܂��B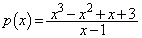 �Ƃ����ƁA
�Ƃ����ƁA 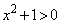 ���A�ȉ��̑����\�������܂�(���̑������Q��)�B�����\�ƁA
���A�ȉ��̑����\�������܂�(���̑������Q��)�B�����\�ƁA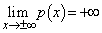 �C
�C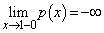 �C
�C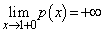 �ɂ��A
�ɂ��A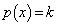 �C�����A
�C�����A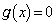 �����قȂ�3�����������̂�
�����قȂ�3�����������̂�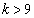 �̂Ƃ��ŁA�@���A
�̂Ƃ��ŁA�@���A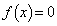 �͑��قȂ�4�̎������������܂��B(�X) 9 ......[��]
�͑��قȂ�4�̎������������܂��B(�X) 9 ......[��]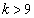 ���A
���A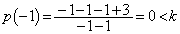 �ł����A����Ƒ����\���A
�ł����A����Ƒ����\���A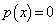 �́A
�́A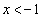 �C
�C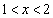 �C
�C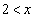 �͈̔͂Ɋe�X1���������A
�͈̔͂Ɋe�X1���������A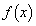 ��4�̉�a�Cb�Cc�Cd (
��4�̉�a�Cb�Cc�Cd (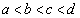 )�ɂ��āA
)�ɂ��āA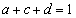 �C
�C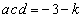
(�Z) 1�@(�\) 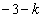 ......[��]
......[��]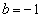 ���A
���A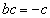
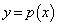 �̃O���t���Q�ߐ�
�̃O���t���Q�ߐ�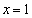 �����̂ŁA
�����̂ŁA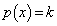 ��
��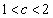 �ƂȂ��c�́A
�ƂȂ��c�́A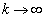 �̂Ƃ��A
�̂Ƃ��A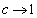 �ƂȂ�܂��B�]���āA
�ƂȂ�܂��B�]���āA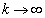 �̂Ƃ��A
�̂Ƃ��A (�^) 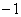 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B