慶大理工数学'12年[2]
円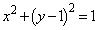 と外接し、x軸と接する円で中心のx座標が正であるものを条件Pを満たす円ということにする。
と外接し、x軸と接する円で中心のx座標が正であるものを条件Pを満たす円ということにする。
(1) 条件Pを満たす円の中心は、曲線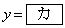 (
(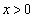 )の上にある。また、条件Pを満たす半径9の円を
)の上にある。また、条件Pを満たす半径9の円を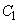 とし、その中心のx座標を
とし、その中心のx座標を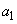 とすると、
とすると、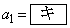 である。
である。 (2) 条件Pを満たし円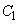 に外接する円を
に外接する円を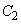 とする。また、
とする。また、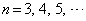 に対し、条件Pを満たし、円
に対し、条件Pを満たし、円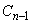 に外接し、かつ円
に外接し、かつ円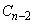 と異なる円を
と異なる円を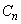 とする。円
とする。円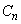 の中心のx座標を
の中心のx座標を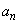 とするとき、自然数nに対し
とするとき、自然数nに対し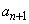 を
を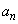 を用いて表しなさい。求める過程も書きなさい。
を用いて表しなさい。求める過程も書きなさい。 (3) (1),(2)で定めた数列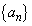 の一般項を求めなさい。求める過程も書きなさい。
の一般項を求めなさい。求める過程も書きなさい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 類題が'92年[A2]でも出題されています。ヒントを活かすことにより、容易に解答できます。
(1) 条件Pを満たす円の中心Dの座標を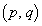 (
(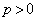 ),点
),点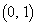 をA,Dからx軸に垂線DHを下ろし、AからDHに垂線ABを下ろします。条件Pを満たす円はx軸に接するので、その半径はqです。
をA,Dからx軸に垂線DHを下ろし、AからDHに垂線ABを下ろします。条件Pを満たす円はx軸に接するので、その半径はqです。 三平方の定理より、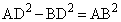
∴ 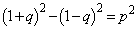 ∴
∴ 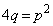 よって、条件Pを満たす円の中心は、曲線
よって、条件Pを満たす円の中心は、曲線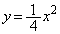 (
(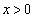 )の上にあります(放物線を参照)。(カ)
)の上にあります(放物線を参照)。(カ) 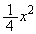 ......[答]条件Pを満たす円の中心のy座標が円の半径なので、
......[答]条件Pを満たす円の中心のy座標が円の半径なので、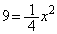 より、
より、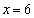
よって、半径9の円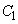 の中心のx座標
の中心のx座標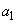 は、
は、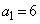 (キ) 6 ......[答]
(キ) 6 ......[答]
(2) nを2以上の整数として、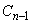 ,
,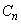 の中心
の中心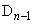 ,
,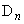 のx座標は
のx座標は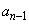 (
(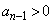 ),
),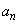 (
(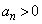 )です。題意より
)です。題意より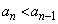 です。条件Pを満たす円の中心は、曲線
です。条件Pを満たす円の中心は、曲線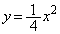 (
(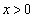 )の上にあるので、
)の上にあるので、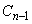 ,
,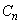 の半径は
の半径は ,
,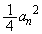 です。
です。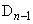 からx軸に垂線
からx軸に垂線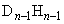 を下ろし、
を下ろし、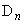 から
から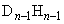 に垂線
に垂線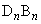 を下ろします。
を下ろします。 よって、nを自然数として、
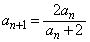 ......[答]
......[答]
(3) (2)の漸化式の逆数を考えると(漸化式の技巧を参照)、 ∴ 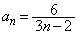 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。