慶應大学理工学部2012年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 3つの行列の積
の成分が任意の実数x，yに対し0以上となるような実数aの範囲を不等式で表すと ア となる。
(2) 
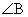が直角の直角三角形ABCの2辺AB，BCの長さをそれぞれ3，1とする。また、
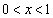を満たすxに対し線分BCを1：xに外分する点をDとする。いま、
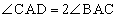が成り立つとすると、
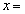イ であり、△ACDの外接円の半径は ウ である。 (3) 関数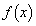
，
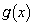が を満たすとき、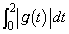
の値は エ または オ である。求める過程も解答欄(3)に書きなさい。 [解答へ]
[2] 円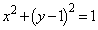
と外接し、x軸と接する円で中心のx座標が正であるものを条件Pを満たす円ということにする。
(1) 条件Pを満たす円の中心は、曲線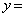
カ (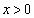
)の上にある。また、条件Pを満たす半径9の円を
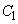とし、その中心のx座標を
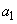とすると、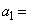
キ である。 (2) 条件Pを満たし円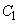
に外接する円を
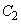とする。また、
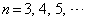に対し、条件Pを満たし、円
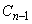に外接し、かつ円
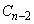と異なる円を
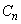とする。円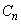
の中心のx座標を
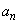とするとき、自然数nに対し
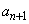を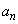
を用いて表しなさい。求める過程も書きなさい。 (3) (1)，(2)で定めた数列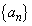
の一般項を求めなさい。求める過程も書きなさい。 [解答へ]
[3] 袋の中に文字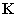
，
，
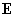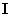が書かれたカードがそれぞれ1枚ずつと、文字
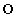が書かれたカードが何枚か入っている。いま、袋の中から1枚ずつカードを取り出し、
，
，
，
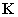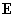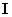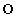のすべての文字のカードがそれぞれ1枚以上出たところで終了する。ただし、一度取り出したカードは袋の中には戻さないものとする。
(1) 袋の中に文字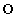
が書かれたカードが7枚あり、合計10枚のカードが入っている場合を考える。3枚目に文字
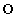のカードを取り出す確率は ク であり、1枚目または3枚目に文字
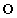のカードを取り出す確率は ケ である。また、最後に取り出したカードに書かれている文字が
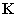である確率は コ である。 (2) 袋の中に文字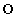
が書かれたカードがn枚 (
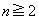)あり、合計
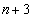枚のカードが入っている場合を考える。k枚目で終了する確率を
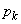とすると、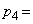
サ であり、
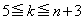に対しては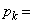
シ である。いま、終了した時点で袋の中に残っているカードの枚数の期待値を
とすると、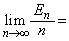
ス が成り立つ。 [解答へ]
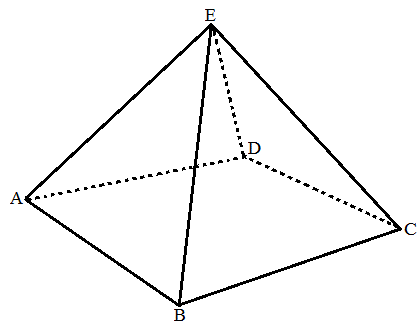[4] ABCDEを1辺の長さが1の正方形ABCDを底面とし、4個の正三角形を側面とする正四角錐とする。
(1) △CDEの重心をGとする。ベクトル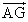
を
，
，
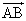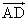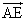で表すと、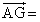
セ となる。 (2) 
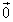でないベクトル
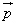が平面α上の任意のベクトルと垂直なとき、
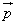は平面αと垂直であるという。
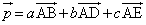(a，b，cは実数)が△CDEを含む平面と垂直なとき、a：b：c ＝ ソ である。よって、
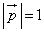かつ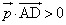
となるようにa，b，cを定めると、
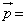タ となる。 [解答へ]
[5]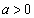 
とし、xの3次関数
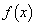を
と定める。また、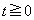
に対し、曲線
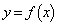とx軸および2直線
，
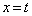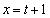で囲まれた部分の面積を
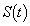で表す。
(1) 
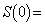ト である。 (2) 
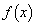は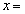
ナ で極小値をとる。曲線
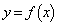上にあり、xの値 ナ に対応する点をPとする。aの値が変化するとき、点Pの軌跡は曲線
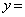ニ (
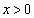)である。 (3)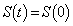 
を満たす正の実数t が存在するようなaの値の範囲を不等式で表すと ヌ となる。以下、aの値はこの範囲にあるとする。cを
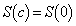を満たす最大の正の実数とする。区間
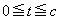における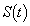
の最大値、最小値をそれぞれ
，
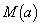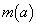とするとき、
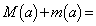ネ となる。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
を
，
，
で表すと、
チ となる。また、Hを辺ECの中点とすると、
ツ であり、△AHFの面積は テ である。