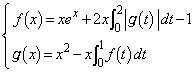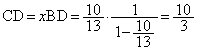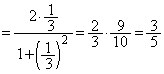�c�嗝�H���w'12�N[1]
(1) 3�̍s��̐�
�̐������C�ӂ̎���x�Cy�ɑ�0�ȏ�ƂȂ�悤�Ȏ���a�͈̔͂�s�����ŕ\�����@�A�@�ƂȂ�B
(2) 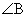 �����p�̒��p�O�p�`ABC��2��AB�CBC�̒��������ꂼ��3�C1�Ƃ���B�܂��A
�����p�̒��p�O�p�`ABC��2��AB�CBC�̒��������ꂼ��3�C1�Ƃ���B�܂��A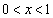 ����x�ɑ�����BC��1�Fx�ɊO������_��D�Ƃ���B���܁A
����x�ɑ�����BC��1�Fx�ɊO������_��D�Ƃ���B���܁A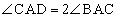 �����藧�Ƃ���ƁA
�����藧�Ƃ���ƁA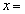 �@�C�@�ł���A��ACD�̊O�ډ~�̔��a���@�E�@�ł���B
�@�C�@�ł���A��ACD�̊O�ډ~�̔��a���@�E�@�ł���B (3) ��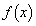 �C
�C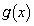 ��
�� �����Ƃ��A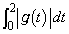 �̒l���@�G�@�܂����@�I�@�ł���B���߂�ߒ�����(3)�ɏ����Ȃ����B
�̒l���@�G�@�܂����@�I�@�ł���B���߂�ߒ�����(3)�ɏ����Ȃ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�܂����A�E�H�[�~���O�E�A�b�v�Ƃ�����b���ł��B
���ꂪ�C�ӂ̎���x�Cy�ɂ��Đ��藧���߂ɁA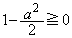 (�A)
(�A) 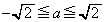 ......[��]
......[��]
�܂��ABD�FCD��1�Fx���A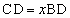 �C
�C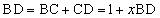 ���A
���A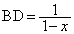
�O�ډ~�̔��aR�́A�����藝���A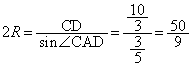 (�E)
(�E) 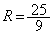 ......[��]
......[��]
(3) 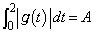 �C
�C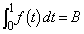 �Ƃ���(��ϕ����Q��)�ƁA
�Ƃ���(��ϕ����Q��)�ƁA ���A
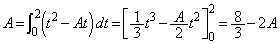 �C
�C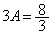
�� 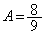 (
(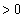 )�C�s�K�B
)�C�s�K�B 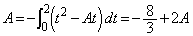 �C
�C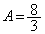 �@����@
�@����@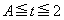 �Ȃ�t �ɂ��āA
�Ȃ�t �ɂ��āA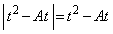
�� 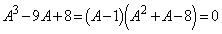
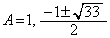
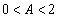 �ƂȂ�̂�
�ƂȂ�̂�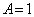 �̂݁@����A
�̂݁@����A�@�C�A���A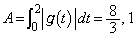 (�G)(�I) 1�C
(�G)(�I) 1�C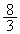 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B