�c�嗝�H���w'12�N[5]
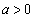 �Ƃ��Ax��3����
�Ƃ��Ax��3����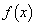 ��
��
�ƒ�߂�B�܂��A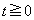 �ɑ��A�Ȑ�
�ɑ��A�Ȑ�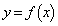 ��x�������2����
��x�������2����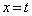 �C
�C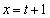 �ň͂܂ꂽ�����̖ʐς�
�ň͂܂ꂽ�����̖ʐς�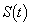 �ŕ\���B
�ŕ\���B
(1) 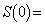 �@�g�@�ł���B
�@�g�@�ł���B (2) 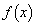 ��
��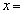 �@�i�@�ŋɏ��l���Ƃ�B�Ȑ�
�@�i�@�ŋɏ��l���Ƃ�B�Ȑ�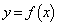 ��ɂ���Ax�̒l�@�i�@�ɑΉ�����_��P�Ƃ���Ba�̒l���ω�����Ƃ��A�_P�̋O�Ղ͋Ȑ�
��ɂ���Ax�̒l�@�i�@�ɑΉ�����_��P�Ƃ���Ba�̒l���ω�����Ƃ��A�_P�̋O�Ղ͋Ȑ�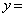 �@�j�@ (
�@�j�@ (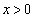 )�ł���B
)�ł���B (3) 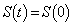 �������̎���t �����݂���悤��a�̒l�͈̔͂�s�����ŕ\�����@�k�@�ƂȂ�B�ȉ��Aa�̒l�͂��͈̔͂ɂ���Ƃ���Bc��
�������̎���t �����݂���悤��a�̒l�͈̔͂�s�����ŕ\�����@�k�@�ƂȂ�B�ȉ��Aa�̒l�͂��͈̔͂ɂ���Ƃ���Bc��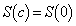 �����ő�̐��̎����Ƃ���B���
�����ő�̐��̎����Ƃ���B���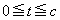 �ɂ�����
�ɂ�����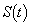 �̍ő�l�A�ŏ��l�����ꂼ��
�̍ő�l�A�ŏ��l�����ꂼ��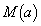 �C
�C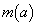 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A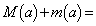 �@�l�@�ƂȂ�B
�@�l�@�ƂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@3����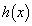 �ɑ��āA
�ɑ��āA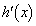 ��2�����ƂȂ�܂�(�������Q��)�B
��2�����ƂȂ�܂�(�������Q��)�B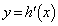 �̃O���t�̎��̈ʒu��
�̃O���t�̎��̈ʒu��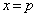 �Ƃ��āA
�Ƃ��āA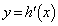 ��
��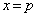 �Ɋւ��đΏ̂Ȃ̂ŁA
�Ɋւ��đΏ̂Ȃ̂ŁA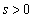 �Ƃ��āA
�Ƃ��āA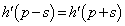 �����藧���܂��B������g���ƁA
�����藧���܂��B������g���ƁA
�ƂȂ�̂ŁA
���A
�� 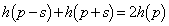
�����藧���܂��B����́A
3�����̃O���t���ϋȓ_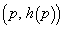 �ɂ��đΏ̂ł��邱�Ɓ@���(��)
�ɂ��đΏ̂ł��邱�Ɓ@���(��)
���Ӗ����܂��B�ȉ�(3)�̉ł́A��������p���Ă݂܂��B
(1)(�g) 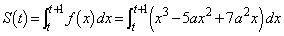
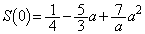 ......[��]
......[��]
(2)(�i) 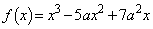
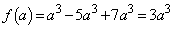 �@����A
�@����A
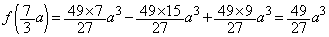 �@����B
�@����B�����\���A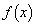 �́A
�́A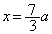 ......[��]�@�ɂ����āA�ɏ��l���Ƃ�܂�(3�����̑������Q��)�B
......[��]�@�ɂ����āA�ɏ��l���Ƃ�܂�(3�����̑������Q��)�B (�j) �_P��x���W�Ay���W�́A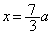 �C
�C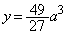
������a���������āA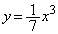 ......[��]�@(
......[��]�@(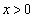 )
)
(3)(�k) 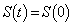 ���A
���A �� 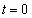 �C
�C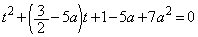
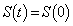 �������̎���t �����݂���̂ŁA
�������̎���t �����݂���̂ŁA �Ƃ����ƁA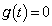 ��2�������������A���̂��߂ɁA
��2�������������A���̂��߂ɁA ���ʎ��F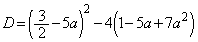
�� 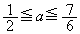 �@����C
�@����C
���K�v�ł��B���̂Ƃ��A������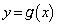 �̎�
�̎�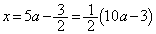 (
(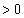 )
) 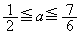 ......[��]
......[��](�l) �C�̂Ƃ��A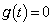 �͏d�����܂߂Đ��̉���2�����A���̂����̑傫������c�ł��B�@���A
�͏d�����܂߂Đ��̉���2�����A���̂����̑傫������c�ł��B�@���A 2��������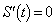 �̔��ʎ�
�̔��ʎ�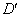 �ɂ��āA
�ɂ��āA �C����������Ƃ��A
�Ȃ̂ŁA2��������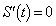 �́A
�́A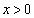 �͈̔͂ɑ��قȂ�2������α�Cβ (
�͈̔͂ɑ��قȂ�2������α�Cβ (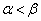 )�������܂��B
)�������܂��B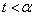 �ɂ�����
�ɂ�����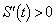 �C
�C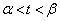 �ɂ�����
�ɂ�����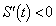 �C
�C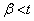 �ɂ�����
�ɂ�����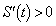 ���A
���A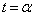 �ɂ�����
�ɂ�����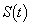 �ɑ�A
�ɑ�A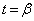 �ɂ�����
�ɂ�����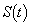 �ɏ��ł��B
�ɏ��ł��B
�܂��A2��������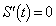 �ɂ��������ƌW���̊W���A
�ɂ��������ƌW���̊W���A 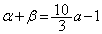 �@����D
�@����D�����ŁA�����A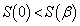 �ł���A
�ł���A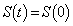 �ƂȂ鐳�̎���t �����݂��Ȃ��Ȃ�̂ŁA
�ƂȂ鐳�̎���t �����݂��Ȃ��Ȃ�̂ŁA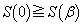 �ł��B�܂�A
�ł��B�܂�A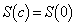 �Ȃ̂�
�Ȃ̂�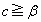 �ł�(3����
�ł�(3����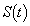 �̃O���t��`���čl���Ă�������)�B�܂��A
�̃O���t��`���čl���Ă�������)�B�܂��A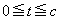 �ɂ�����
�ɂ�����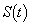 �̍ŏ��l
�̍ŏ��l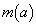 ��
��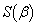 �ł��B
�ł��B
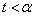 �ɂ����Ă�
�ɂ����Ă�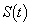 �͑����Ȃ̂ŁA
�͑����Ȃ̂ŁA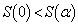 �ł����āA
�ł����āA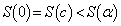 �Ȃ̂ŁA
�Ȃ̂ŁA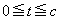 �ɂ�����
�ɂ�����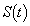 �̍ő�l
�̍ő�l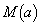 ��
��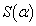 �ł��B�ȏ���A
�ł��B�ȏ���A �ƂȂ�܂��B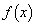 ��3�����Ȃ̂ŁA��L(��)�̂悤�ɁA
��3�����Ȃ̂ŁA��L(��)�̂悤�ɁA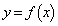 �̃O���t�͂��̕ϋȓ_�Ɋւ��đΏ̂ł��B
�̃O���t�͂��̕ϋȓ_�Ɋւ��đΏ̂ł��B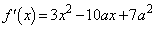 ���A
���A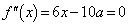 �Ƃ���ƁA
�Ƃ���ƁA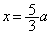 �C�]���āA
�C�]���āA 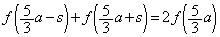 �@����E
�@����E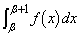 �ɂ����āA
�ɂ����āA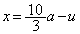 (
(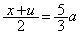 )�Ƃ����ƁA�D��p���āA
)�Ƃ����ƁA�D��p���āA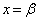 �̂Ƃ�
�̂Ƃ�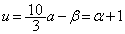 �C
�C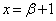 �̂Ƃ�
�̂Ƃ�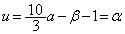 ���A
���A�� 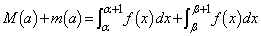
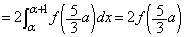 (= ���)
(= ���)�܂��A�E�ɂ����āA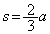 �Ƃ��邱�Ƃɂ��A�A�C�B��p���āA
�Ƃ��邱�Ƃɂ��A�A�C�B��p���āA 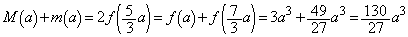 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B