�c�嗝�H���w'13�N[1]
���W���ʏ�ɂ����āA������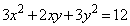 �ŕ\�����}�`C���l����B�s��
�ŕ\�����}�`C���l����B�s��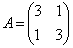 ��p����ƁA���̕�������
��p����ƁA���̕������� 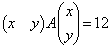 �ƕ\����B
�ƕ\����B
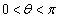 �ł���θ ��p���āA
�ł���θ ��p���āA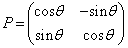 �ƕ\�����s��P���A�������α�Cβ (
�ƕ\�����s��P���A�������α�Cβ (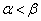 )�ɑ��A
)�ɑ��A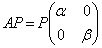 �����Ƃ���B���̂Ƃ��A
�����Ƃ���B���̂Ƃ��A �ł���A
�ł���A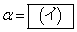 �C
�C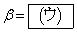 �ł���B
�ł���B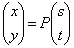 �Ƃ����ƁA�}�`C�̕�����
�Ƃ����ƁA�}�`C�̕�����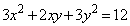 ��
��
�ƂȂ�B
�}�`C���2�_�Ԃ̋����̍ő�l�� �ł���A���̍ő�l��^����}�`C���2�_�̍��W��
�ł���A���̍ő�l��^����}�`C���2�_�̍��W�� ��
��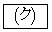 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2009�N[B1]�ł��o�肳�ꂽ�x�N�g���̑傫����ς��Ȃ�1���ϊ�(�s�����2�̃x�N�g���ƌ���Ƃ��A����2�̃x�N�g������������̂Łu����ϊ��v�ƌ����܂�)�̖��ł��B�x�N�g���̑傫����ς��Ȃ�1���ϊ��́A�{��́u��]�ϊ��v�ƁA2011�N[A1]�ł��o�肳�ꂽ�����Ɋւ���Ώ̈ړ�(�u���f�ϊ��v�ƌ����܂�)��2�ʂ肠�邱�Ƃ��m���Ă��܂��B
�� 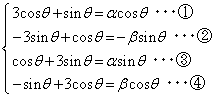
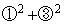 ���A
���A
�� 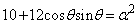 �@����D
�@����D
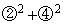 ���A
���A
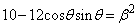 �@����E
�@����E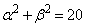 �@����F
�@����F
�@�{�C���A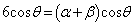 �@����G
�@����G
�B�|�A���A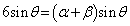 �@����H
�@����H
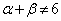 ���Ƃ���ƁA�G�C�H���A
���Ƃ���ƁA�G�C�H���A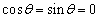 �ƂȂ��Ă��܂��̂ŕs�K�B
�ƂȂ��Ă��܂��̂ŕs�K�B
����āA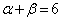 �C����ƇF���
�C����ƇF���
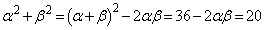 �@��
�@�� 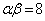
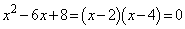 ��2���ŁA
��2���ŁA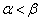 ���A
���A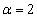 �C
�C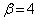
���̂Ƃ��A�G�C�H���A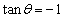 �C
�C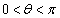 ���
���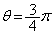
(�A) 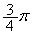 �@(�C) 2�@(�E) 4 ......[��]
�@(�C) 2�@(�E) 4 ......[��]
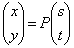 �Ƃ����ƁA
�Ƃ����ƁA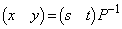 (�t�s�����Q��)�ŁA
(�t�s�����Q��)�ŁA
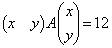 �ƁA
�ƁA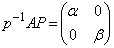 �Ƃ���A
�Ƃ���A
�� 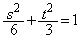 �@(�ȉ~���Q��)
�@(�ȉ~���Q��)
(�G) 6�@(�I) 3 ......[��]
���D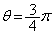 �̂Ƃ��A
�̂Ƃ��A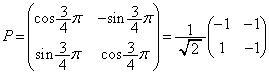 ���A
���A ���A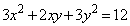 �ɑ�����āA
�ɑ�����āA �� 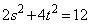 �Ƃ��邱�Ƃ��ł��܂��B
�Ƃ��邱�Ƃ��ł��܂��B �}�`C���2�_�Ԃ̋����̍ő�l�͒����̒���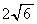 �ŁA�����^����2�_�͒����̗��[�A
�ŁA�����^����2�_�͒����̗��[�A
����ƁA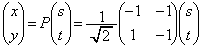 ���A
���A
(�J) 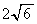 �@(�L)
�@(�L) 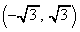 �@(�N)
�@(�N) 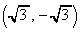 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 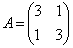 ��p����ƁA���̕�������
��p����ƁA���̕������� 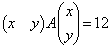 �ƕ\����B
�ƕ\����B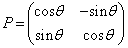 �ƕ\�����s��P���A�������α�Cβ (
�ƕ\�����s��P���A�������α�Cβ (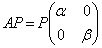 �����Ƃ���B���̂Ƃ��A
�����Ƃ���B���̂Ƃ��A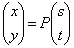 �Ƃ����ƁA�}�`C�̕�����
�Ƃ����ƁA�}�`C�̕�����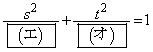
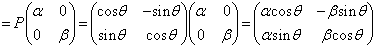
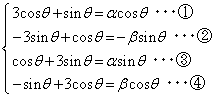
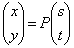 �Ƃ����ƁA
�Ƃ����ƁA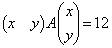 �ƁA
�ƁA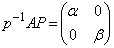 �Ƃ���A
�Ƃ���A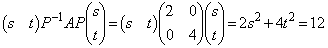
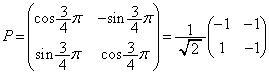 ���A
���A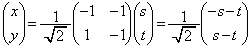
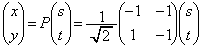 ���A
���A