�c�嗝�H���w'21�N[3]
n�����R���Ƃ���B1�̂���������J��Ԃ�������������s���A�J��Ԃ���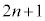 ��ɒB���邩�A5�ȏ�̖ڂ�2��A�����ďo���ꍇ�Ɏ������I������B���̕\�́A
��ɒB���邩�A5�ȏ�̖ڂ�2��A�����ďo���ꍇ�Ɏ������I������B���̕\�́A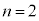 �̏ꍇ�̗�ł���B��a�ł́A5�ȏ�̖ڂ�2��A�����ďo���A5��Ŏ������I�������B��b�ł́A5�ȏ�̖ڂ�2��A�����ďo�����߁A3��Ŏ������I�������B
�̏ꍇ�̗�ł���B��a�ł́A5�ȏ�̖ڂ�2��A�����ďo���A5��Ŏ������I�������B��b�ł́A5�ȏ�̖ڂ�2��A�����ďo�����߁A3��Ŏ������I�������B
| �@ | 1��� | 2��� | 3��� | 4��� | 5��� |
| ��a | 4 | 6 | 1 | 2 | 1 |
| ��b | 3 | 6 | 5 | �@ | �@ |
���̎����ɂ����āAA���u5�ȏ�̖ڂ�2��A�����ďo��v���ہA�̐���k�ɑ�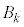 ���u5�����̖ڂ��o�������傤��k�ł���v���ۂƂ���B��ʂɁA����C�̊m����
���u5�����̖ڂ��o�������傤��k�ł���v���ۂƂ���B��ʂɁA����C�̊m����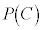 �CC���N�������Ƃ��̎���D���N��������t���m����
�CC���N�������Ƃ��̎���D���N��������t���m����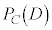 �ƕ\���B
�ƕ\���B
(1) 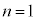 �̂Ƃ��A
�̂Ƃ��A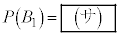 �ł���B
�ł���B
(2) 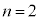 �̂Ƃ��A
�̂Ƃ��A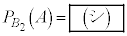 �ł���B
�ł���B
�ȉ��A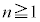 �Ƃ���B
�Ƃ���B
(3) 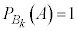 �ƂȂ�k�̒l�͈̔͂́A
�ƂȂ�k�̒l�͈̔͂́A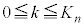 �ƕ\�����Ƃ��ł���B����
�ƕ\�����Ƃ��ł���B����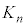 ��n�̎��ŕ\����
��n�̎��ŕ\����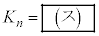 �ł���B
�ł���B
(4) 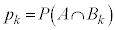 �Ƃ����B
�Ƃ����B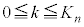 �̂Ƃ��A
�̂Ƃ��A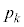 �����߂��
�����߂��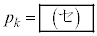 �ł���B�܂��A
�ł���B�܂��A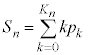 �Ƃ�����
�Ƃ�����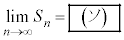 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ڂ̏o���ɂ��Ă�������}��`���āA��ӂ��悭����ʼn���悤�ɂ���K�v������܂��B
(1) 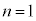 �̂Ƃ��A�J�Ԃ��͍ő�
�̂Ƃ��A�J�Ԃ��͍ő�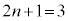 ��ł��B
��ł��B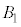 ��5�����̖ڂ����傤��1��o�鎖�ۂł��B1, 2, 3, 4�̖ڂ��o�鎖��(�m��
��5�����̖ڂ����傤��1��o�鎖�ۂł��B1, 2, 3, 4�̖ڂ��o�鎖��(�m��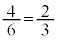 )�����A5, 6�̖ڂ��o�鎖��(�m��
)�����A5, 6�̖ڂ��o�鎖��(�m��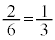 )�����ŕ\��(����2���Ǝ����I��)�ƁA
)�����ŕ\��(����2���Ǝ����I��)�ƁA ����āA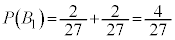 ......[�T]
......[�T]
(2) 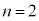 �̂Ƃ��A�J��Ԃ��͍ő�
�̂Ƃ��A�J��Ԃ��͍ő�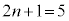 ��ł��B
��ł��B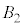 ��5�����̖ڂ����傤��2��o�鎖�ۂł��B
��5�����̖ڂ����傤��2��o�鎖�ۂł��B ���������@�@�m��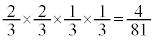 �@����@
�@����@
�����������@�m��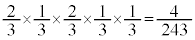 �@����A
�@����A
�����������@�m��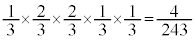 �@����B
�@����B
�����������@�m��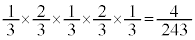 �@����C
�@����C ������A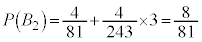
���̂����ŁA����A�̏����F�u5�ȏ�̖ڂ�2��A������v����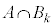 �ɓ���̂́A�Ō��3�������ƂȂ�@�C�A�C�B�ŁA
�ɓ���̂́A�Ō��3�������ƂȂ�@�C�A�C�B�ŁA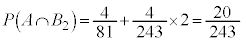
�����(�����t���m�����Q��)�A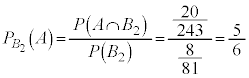 ......[�V]
......[�V]
(3) 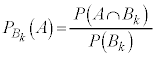 �Ȃ̂ŁA
�Ȃ̂ŁA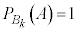 �Ƃ������Ƃ́A
�Ƃ������Ƃ́A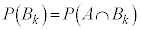 �Ƃ������Ƃł��B(2)�ł́A
�Ƃ������Ƃł��B(2)�ł́A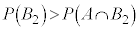 �ɂȂ��Ă��܂����A����͇C�̏ꍇ�A�܂�A�Ō��3��'������'�ɂȂ��Ă��Ȃ��ꍇ�����邩��ł��B
�ɂȂ��Ă��܂����A����͇C�̏ꍇ�A�܂�A�Ō��3��'������'�ɂȂ��Ă��Ȃ��ꍇ�����邩��ł��B '����'�Ŏ����͏I�����܂��B�܂��A����3�����Ƃ͂Ȃ��̂ŁA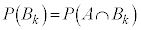 �ƂȂ邽�߂ɂ́A�Ō��3���'������'�łȂ�������܂���B
�ƂȂ邽�߂ɂ́A�Ō��3���'������'�łȂ�������܂���B
�����ƌ���������ƁA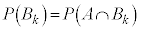 �C�����A
�C�����A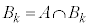 �C�܂�
�C�܂�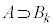 �ƂȂ�̂́A�u5�����̖ڂ��o�������傤��k�ł���v�Ƃ��͕K���u5�ȏ�̖ڂ�2��A�����ďo��v�Ƃ������Ƃł��B
�ƂȂ�̂́A�u5�����̖ڂ��o�������傤��k�ł���v�Ƃ��͕K���u5�ȏ�̖ڂ�2��A�����ďo��v�Ƃ������Ƃł��B
�����͍ő�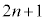 ��J��Ԃ���܂��B����k��N����܂����A�����̍Ō��3���'������'�ŁA�����܂łɁ���
��J��Ԃ���܂��B����k��N����܂����A�����̍Ō��3���'������'�ŁA�����܂łɁ���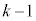 ��C���͍ő�k��(������n�܂��ā��Ɓ������݂ɋN���čŌオ���̂Ƃ�)�N����̂ŁA
��C���͍ő�k��(������n�܂��ā��Ɓ������݂ɋN���čŌオ���̂Ƃ�)�N����̂ŁA ��������ő�̐���k��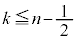 �C����āA
�C����āA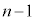 ......[�X]
......[�X]
(4) (3)���A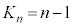 ��
��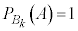 �ł����A
�ł����A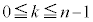 ��
��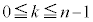 ���ǂ����͂킩��܂���B
���ǂ����͂킩��܂���B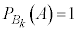 �́A�u5�ȏ�̖ڂ�2��A�����ďo��v���u5�����̖ڂ��o�������傤��k�ł���v�m���ł��B
�́A�u5�ȏ�̖ڂ�2��A�����ďo��v���u5�����̖ڂ��o�������傤��k�ł���v�m���ł��B 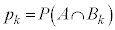 �̂Ƃ��A
�̂Ƃ��A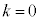 �́A5�ȏ�̖ڂ�2��A�����ďo�āA5�����̖ڂ�0��o��ꍇ�ŁA
�́A5�ȏ�̖ڂ�2��A�����ďo�āA5�����̖ڂ�0��o��ꍇ�ŁA�����@�m��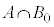 �C����āA
�C����āA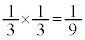
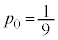 �̂Ƃ��A
�̂Ƃ��A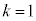 �́A5�ȏ�̖ڂ�2��A�����ďo�āA5�����̖ڂ�1��o��ꍇ�ŁA
�́A5�ȏ�̖ڂ�2��A�����ďo�āA5�����̖ڂ�1��o��ꍇ�ŁA�������@�@�m��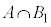 �@����D
�@����D
���������@�m��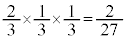 �@����E
�@����E
����āA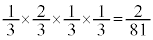
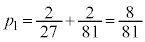 �̂Ƃ��A
�̂Ƃ��A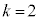 �́A5�ȏ�̖ڂ�2��A�����ďo�āA5�����̖ڂ�2��o��ꍇ�ŁA
�́A5�ȏ�̖ڂ�2��A�����ďo�āA5�����̖ڂ�2��o��ꍇ�ŁA���������@�@�@�m��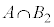 �@����F�����������@�@�m��
�@����F�����������@�@�m��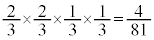 �@����G
�@����G
�����������@�@�m��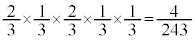 �@����H
�@����H
�������������@�m��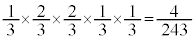 �@����I
�@����I
����āA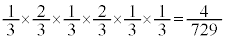
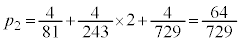 �̏ꍇ��
�̏ꍇ��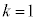 �̏ꍇ���r����ƁA�D��'������'�̑O��'��'���t���ƇF�C'����'���t���ƇG�ɂȂ�܂��B�E�̍ŏ��́��̂��Ƃ�'��'���t���ƇH�C'����'���t���ƇI�ɂȂ�܂��B'��'�̊m����
�̏ꍇ���r����ƁA�D��'������'�̑O��'��'���t���ƇF�C'����'���t���ƇG�ɂȂ�܂��B�E�̍ŏ��́��̂��Ƃ�'��'���t���ƇH�C'����'���t���ƇI�ɂȂ�܂��B'��'�̊m����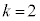 �C'����'�̊m����
�C'����'�̊m����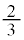 �C���킹��
�C���킹��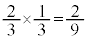 �C
�C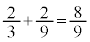 �ƂȂ��Ă��܂��B
�ƂȂ��Ă��܂��B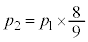 �̏ꍇ��
�̏ꍇ��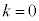 �̏ꍇ�̊Ԃɂ��A
�̏ꍇ�̊Ԃɂ��A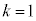 �Ƃ����W������܂��B
�Ƃ����W������܂��B
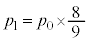 �̏ꍇ��
�̏ꍇ��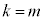 �̏ꍇ���r���Ă��A���̉�1����ƁA'��'�̂�1����ꍇ�ƁA'��'��'��'��1��������ꍇ�Ƃ�����A'��'��'����'���킹�Ċm����
�̏ꍇ���r���Ă��A���̉�1����ƁA'��'�̂�1����ꍇ�ƁA'��'��'��'��1��������ꍇ�Ƃ�����A'��'��'����'���킹�Ċm����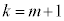 �Ȃ̂ŁA
�Ȃ̂ŁA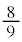 �ƂȂ�܂��B
�ƂȂ�܂��B
�ȏ���A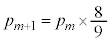 �͏���
�͏���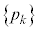 �C����
�C����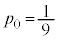 �����䐔���ŁA
�����䐔���ŁA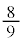 ......[�Z]
......[�Z]�J�|�K���A
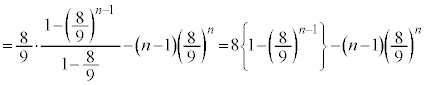 �̂Ƃ��A
�̂Ƃ��A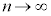 �C
�C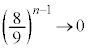 ���A
���A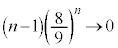
�� 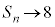 ......[�\]
......[�\]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 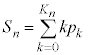 �Ƃ�����
�Ƃ�����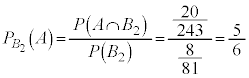 ......[�V]
......[�V]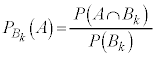 �Ȃ̂ŁA
�Ȃ̂ŁA