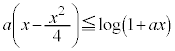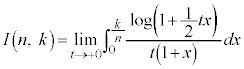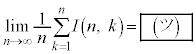慶應大学理工学部2021年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] t を実数とし、座標平面上の直線l: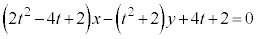 を考える。
を考える。
(1) 直線lはt の値によらず、定点を通る。その定点の座標は である。
である。
(2) 直線lの傾きを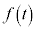 とする。
とする。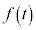 の傾きが最小となるのは
の傾きが最小となるのは のときであり、最大となるのは
のときであり、最大となるのは のときである。また、aを実数とするとき、t に関する方程式
のときである。また、aを実数とするとき、t に関する方程式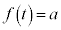 がちょうど1個の実数解をもつようなaの値をすべて求めると、
がちょうど1個の実数解をもつようなaの値をすべて求めると、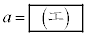 である。
である。
(3) t が実数全体を動くとき、直線lが通過する領域をSとする。また、kを実数とする。放物線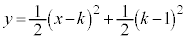 が領域Sと共有点を持つようなkの値の範囲は
が領域Sと共有点を持つようなkの値の範囲は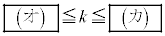 である。
である。 [解答へ]
[2](1) 複素数αは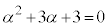 を満たすとする。このとき、
を満たすとする。このとき、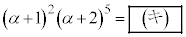 である。また、
である。また、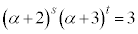 となる整数s,tの組をすべて求め、求める過程とともに解答欄(1)に記述しなさい。
となる整数s,tの組をすべて求め、求める過程とともに解答欄(1)に記述しなさい。
(2) 多項式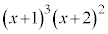 を
を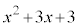 で割ったときの商は
で割ったときの商は ,余りは
,余りは である。また、
である。また、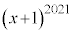 を
を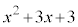 で割ったときの余りは
で割ったときの余りは である。
である。 [解答へ]
[3] nを自然数とする。1個のさいころを繰り返し投げる実験を行い、繰り返す回数が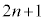 回に達するか、5以上の目が2回連続して出た場合に実験を終了する。下の表は、
回に達するか、5以上の目が2回連続して出た場合に実験を終了する。下の表は、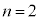 の場合の例である。例aでは、5以上の目が2回連続して出ず、5回で実験を終了した。例bでは、5以上の目が2回連続して出たため、3回で実験を終了した。
の場合の例である。例aでは、5以上の目が2回連続して出ず、5回で実験を終了した。例bでは、5以上の目が2回連続して出たため、3回で実験を終了した。
| | 1回目 | 2回目 | 3回目 | 4回目 | 5回目 |
| 例a | 4 | 6 | 1 | 2 | 1 |
| 例b | 3 | 6 | 5 | | |
この実験において、Aを「5以上の目が2回連続して出る」事象、非負の整数kに対し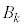 を「5未満の目が出た回数がちょうどkである」事象とする。一般に、事象Cの確率を
を「5未満の目が出た回数がちょうどkである」事象とする。一般に、事象Cの確率を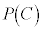 ,Cが起こったときの事象Dが起こる条件付き確率を
,Cが起こったときの事象Dが起こる条件付き確率を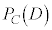 と表す。
と表す。
(1) 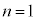 のとき、
のとき、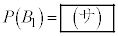 である。
である。
(2) 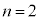 のとき、
のとき、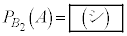 である。
である。
以下、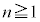 とする。
とする。
(3) 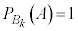 となるkの値の範囲は、
となるkの値の範囲は、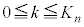 と表すことができる。この
と表すことができる。この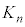 をnの式で表すと
をnの式で表すと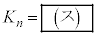 である。
である。
(4) 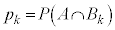 とおく。
とおく。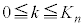 のとき、
のとき、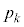 を求めると
を求めると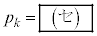 である。また、
である。また、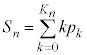 とおくと
とおくと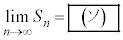 である。
である。 [解答へ]
[4](1) aは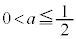 を満たす定数とする。
を満たす定数とする。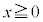 の範囲で不等式
の範囲で不等式
が成り立つことを示しなさい。
(2) bを実数の定数とする。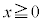 の範囲で不等式
の範囲で不等式 が成り立つようなbの最小値は である。
である。
(3) nとkを自然数とし、
とおく。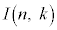 を求めると、
を求めると、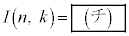 である。また
である。また である。
[解答へ]
[5] 座標平面上で、原点Oを通り、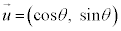 を方向ベクトルとする直線をlとおく。ただし、
を方向ベクトルとする直線をlとおく。ただし、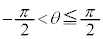 とする。
とする。
(1) 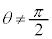 とする。直線lの法線ベクトルで、y成分が正であり、大きさが1のベクトルを
とする。直線lの法線ベクトルで、y成分が正であり、大きさが1のベクトルを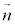 とおく。点P
とおく。点P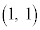 に対し、
に対し、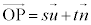 と表す。
と表す。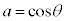 ,
,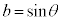 として、s,tのそれぞれをa,bについての1次式で表すと
として、s,tのそれぞれをa,bについての1次式で表すと ,
, である。
である。
点P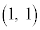 から直線lに垂線を下ろし、直線lとの交点をQとする。ただし、点Pが直線l上にあるときは、点QはPとする。以下では、
から直線lに垂線を下ろし、直線lとの交点をQとする。ただし、点Pが直線l上にあるときは、点QはPとする。以下では、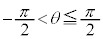 とする。
とする。
(2) 線分PQの長さは、 のとき最大となる。
のとき最大となる。
さらに、点R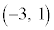 から直線lに垂線を下ろし、直線lとの交点をSとする。ただし、点Rが直線l上にあるときは、点SはRとする。
から直線lに垂線を下ろし、直線lとの交点をSとする。ただし、点Rが直線l上にあるときは、点SはRとする。
(3) 線分QSを1:3に内分する点をTとおく。θが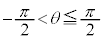 を満たしながら動くとき、点T
を満たしながら動くとき、点T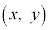 がえがく軌跡の方程式は
がえがく軌跡の方程式は である。
である。
(4) 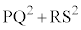 の最大値は
の最大値は である。
である。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 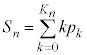 とおくと
とおくと